题目内容
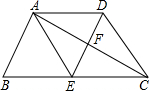 如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED,AC与ED相交于点F.求证:梯形ABCD是等腰梯形.
如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED,AC与ED相交于点F.求证:梯形ABCD是等腰梯形.考点:等腰梯形的判定,全等三角形的判定与性质
专题:证明题
分析:首先根据平行线的性质可得∠DEC=∠EDA,∠BEA=∠EAD,然后再证明∠DEC=∠AEB,可证明△DEC≌△AEB,根据全等三角形的性质可得AB=CD,进而得到梯形ABCD是等腰梯形.
解答:证明:∵AD∥BC,
∴∠DEC=∠EDA,∠BEA=∠EAD.
又∵EA=ED,
∴∠EAD=∠EDA.
∴∠DEC=∠AEB.
又∵EB=EC,
在△DEC和△AEB中,
,
∴△DEC≌△AEB(SAS).
∴AB=CD.
∴梯形ABCD是等腰梯形.
∴∠DEC=∠EDA,∠BEA=∠EAD.
又∵EA=ED,
∴∠EAD=∠EDA.
∴∠DEC=∠AEB.
又∵EB=EC,
在△DEC和△AEB中,
|
∴△DEC≌△AEB(SAS).
∴AB=CD.
∴梯形ABCD是等腰梯形.
点评:此题主要考查了等腰梯形的判定,关键是找出证明△DEC≌△AEB的条件,从而得到AB=CD.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
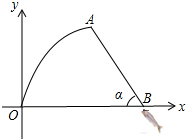 某市举行钓鱼比赛,如图,选手甲钓到了一条大鱼,鱼竿被拉弯近似可看作以A为最高点的一条抛物线,鱼线AB长6m,鱼隐约在水面了,估计鱼离鱼竿支点有8m,此时鱼竿鱼线呈一个平面,且与水平面夹脚α恰好为60°,以鱼竿支点为原点,求鱼竿所在抛物线的解析式.
某市举行钓鱼比赛,如图,选手甲钓到了一条大鱼,鱼竿被拉弯近似可看作以A为最高点的一条抛物线,鱼线AB长6m,鱼隐约在水面了,估计鱼离鱼竿支点有8m,此时鱼竿鱼线呈一个平面,且与水平面夹脚α恰好为60°,以鱼竿支点为原点,求鱼竿所在抛物线的解析式.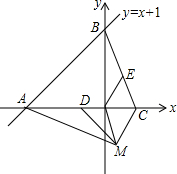 如图,在平面直角坐标系中直线y=x+1与坐标轴交于AB两点,AB=AC,D、E分别为AC、BC的中点,作∠CDM=45°,AM⊥CM,
如图,在平面直角坐标系中直线y=x+1与坐标轴交于AB两点,AB=AC,D、E分别为AC、BC的中点,作∠CDM=45°,AM⊥CM,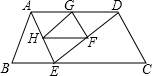 如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AB=2,AD=3,点E是线段BC上的一个动点(E与B、C不重合),G、F、H分别是AD、DE、AE的中点,连接HG、GF、FH.
如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AB=2,AD=3,点E是线段BC上的一个动点(E与B、C不重合),G、F、H分别是AD、DE、AE的中点,连接HG、GF、FH. 如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,
如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,