题目内容
3．已知直角三角形的两直角边分别为8和15，则这个三角形的内切圆的直径为6．分析 先利用勾股定理计算出斜边，然后利用直角三角形的内切圆的半径r=$\frac{a+b-c}{2}$（a、b为直角边，c为斜边）计算出圆的内切圆的半径，从而得到内切圆的直径．
解答 解：直角三角形的斜边=$\sqrt{1{5}^{2}+{8}^{2}}$=17，
所以这个三角形的内切圆的半径=$\frac{8+15-17}{2}$=3，
所以这个三角形的内切圆的直径为6．
故答案为6．
点评 本题考查了三角形的内切圆与内心：三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．记住直角三角形的内切圆的半径r=$\frac{a+b-c}{2}$（a、b为直角边，c为斜边）．
练习册系列答案
相关题目
14．下列各式是最简二次根式的是（ ）
| A． | $\sqrt{12}$ | B． | $\sqrt{{x}^{2}+1}$ | C． | $\sqrt{0.5}$ | D． | $\sqrt{\frac{5}{3}}$ |
18．小李有2根木棒，长度分别为10cm和15cm，要组成一个三角形（木棒的首尾分别相连接），还需在下列4根木棒中选取（ ）
| A． | 4cm长的木棒 | B． | 5cm长的木棒 | C． | 20cm长的木棒 | D． | 25cm长的木棒 |
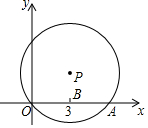如图所示，在平面直角坐标系中，点P在第一象限，⊙P与x轴交于O、A两点，点B是OA的中点，点B的坐标为（3，0），⊙P的半径为$\sqrt{13}$，则点P的坐标为（3，2）．