题目内容
13．已知3x-6a＜9有4个正整数解，则a的取值范围$\frac{1}{2}$＜a≤1．分析 首先求得不等式3x-6a＜9的解集，根据不等式的正整数解即可得到一个关于a的不等式组，即可求得a的范围．
解答 解：解一元一次不等式3x-6a＜9得：x＜2a+3不等式有4个正整数，则最大的一个一定是4．
根据题意得：4＜2a+3≤5
解得：$\frac{1}{2}$＜a≤1
故答案是：$\frac{1}{2}$＜a≤1．
点评 此题考查了一元一次不等式点整数解，比较简单，根据x的取值范围确定2a+3的范围是解题的关键．在解不等式时要根据不等式的基本性质．
练习册系列答案
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案
相关题目
3．若点（-2，y1），（ 1，y2），（ 2，y3）都在反比例函数y=-$\frac{1}{x}$的图象上，则有（ ）
| A． | y1＞y2＞y3 | B． | y1＞y3＞y2 | C． | y3＞y1＞y2 | D． | y2＞y1＞y3 |
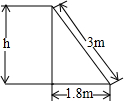如图，一架长3m的梯子斜靠在墙上，梯子的底端到墙角的距离为1.8m，则梯子顶端到地面的距离h为2.4m．
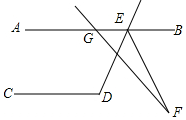如图，AB∥CD，∠CDE=116°，GF交∠DEB的平分线EF于点F，∠AGF=130°，则∠F=8°．