题目内容
9.《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①)
阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求间径就是要求⊙O的直径.
再次阅读后,发现AB=1寸,CD=10寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件,并帮助小智求出⊙O的直径.
分析 根据题意容易得出AB和CD的长;连接OB,设半径CO=OB=x寸,先根据垂径定理求出CA的长,再根据勾股定理求出x的值,即可得出直径.
解答 解:根据题意得:AB=1寸,CD=10寸;
故答案为:1,10;
(2)连接CO,如图所示: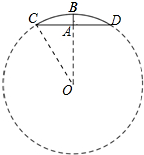
∵BO⊥CD,
∴$CA=\frac{1}{2}CD=5$.
设CO=OB=x寸,则AO=(x-1)寸,
在Rt△CAO中,∠CAO=90°,
∴AO2+CA2=CO2.
∴(x-1)2+52=x2.
解得:x=13,
∴⊙O的直径为26寸.
点评 本题考查了勾股定理在实际生活中的应用;根据题意作出辅助线,构造出直角三角形,运用勾股定理得出方程是解答此题的关键.

练习册系列答案
相关题目
20.下列方程中,无实数根的方程是( )
| A. | x2+1=0 | B. | x2+x=0 | C. | x2+x-1=0 | D. | x2=0 |
14.单项式-$\frac{{x}^{3}y}{2}$的系数是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -1 | D. | 1 |
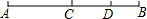 如图线段AB,C是线段AB的中点,点D在CB上,且AD=6.5cm,DB=1.5cm,则线段CD=2.5cm.
如图线段AB,C是线段AB的中点,点D在CB上,且AD=6.5cm,DB=1.5cm,则线段CD=2.5cm.
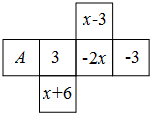 如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体相对的两个面所标注的值均互为相反数,求字母A所标注的值.
如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体相对的两个面所标注的值均互为相反数,求字母A所标注的值.