题目内容
17.我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图所示)就是一例.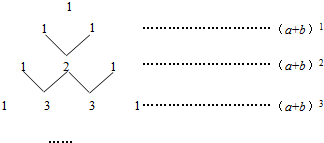
这个三角形的构造法则为:两腰上的数都是1,其余每个数均为其上方左右两数之和.事实上,这个三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数等等.根据上面的规律,(a+b)4的展开式中各项系数最大的数为6;式子75+5×74×(-5)+10×73×(-5)2+10×72×(-5)3+5×7×(-5)4+(-5)5的值为32.
分析 根据三角形的构造法则,确定出(a+b)4的展开式中各项系数最大的数;原式变形后,计算即可得到结果.
解答 解:根据题意得:(a+b)4的展开式中各项系数分别为1,4,6,4,1,即最大的数为6;
75+5×74×(-5)+10×73×(-5)2+10×72×(-5)3+5×7×(-5)4+(-5)5=(7-5)5=32.
故答案为:6;32.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
5.分解因式8a2-8ab+2b2结果正确的是( )
| A. | 2(2a-b)2 | B. | 8(a-b)2 | C. | 4(a-b)2 | D. | 2(2a+b)2 |
 如图,已知 AB∥CD∥EF,AB:CD:EF=2:3:5,$\overrightarrow{BF}$=$\overrightarrow{a}$,
如图,已知 AB∥CD∥EF,AB:CD:EF=2:3:5,$\overrightarrow{BF}$=$\overrightarrow{a}$,