题目内容
10. 如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )
如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )| A. | $5\sqrt{3}$米 | B. | 10米 | C. | 15米 | D. | 10$\sqrt{3}$米 |
分析 Rt△ABC中,已知坡比是坡面的铅直高度BC与水平宽度AC之比,通过解直角三角形即可求出水平宽度AC的长.
解答 解:∵Rt△ABC中,BC=5$\sqrt{3}$米,tanA=$\frac{{\sqrt{3}}}{3}$;
∴AC=BC÷tanA=15米;
故选C.
点评 此题主要考查学生对坡度坡角的掌握及三角函数的运用能力,熟练运用勾股定理是解答本题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
1.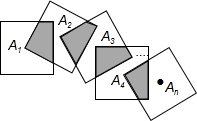 如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )
如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )
 如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )
如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )| A. | n | B. | n-1 | C. | 4(n-1) | D. | 4n |
15.一个几何体的三视图如图所示,则这个几何体可能是( )


| A. | 圆锥 | B. | 球 | C. | 圆柱 | D. | 圆 |
2. 画函数y=2x+1的图象(先填下表,再在图中的直角坐标系中描点,连线)
画函数y=2x+1的图象(先填下表,再在图中的直角坐标系中描点,连线)
 画函数y=2x+1的图象(先填下表,再在图中的直角坐标系中描点,连线)
画函数y=2x+1的图象(先填下表,再在图中的直角坐标系中描点,连线) | x | -2.5 | -2 | -1 | 0 | 1 | 2 | 2.5 |
| y |
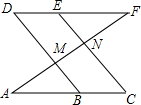 如图.已知∠D=∠C,∠AMB=∠ENF,求证:DF∥AC.
如图.已知∠D=∠C,∠AMB=∠ENF,求证:DF∥AC. 如图,在△ABC中,AB=20,AC=30,∠BAC=120°,求S△ABC的值.
如图,在△ABC中,AB=20,AC=30,∠BAC=120°,求S△ABC的值.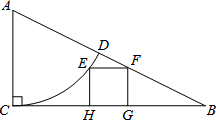 如图,Rt△ABC中,∠ACB=90°,AC=5,CB=10.以点A为圆心,AC长为半径的弧CD交AB于点D,点E是弧CD上任意一点,EH⊥BC于点H,以EH为边长作正方形EHGF,点F在AB边上,则S正方形EFGH=4.
如图,Rt△ABC中,∠ACB=90°,AC=5,CB=10.以点A为圆心,AC长为半径的弧CD交AB于点D,点E是弧CD上任意一点,EH⊥BC于点H,以EH为边长作正方形EHGF,点F在AB边上,则S正方形EFGH=4. 已知△ABC中,∠BAC=90°,四边形ABDE、BCFG是两个正方形,AB的延长线交DG于P,求证:AC=2BP.
已知△ABC中,∠BAC=90°,四边形ABDE、BCFG是两个正方形,AB的延长线交DG于P,求证:AC=2BP.