题目内容
1. 如图所示,ABCD为正方形,延长AD到E,使DE=AD,FG∥BD,EG交AF于H,证明:HD=AD.
如图所示,ABCD为正方形,延长AD到E,使DE=AD,FG∥BD,EG交AF于H,证明:HD=AD.
分析 根据题意先证出△FGC是等腰直角三角形,得出BF=DG,由SAS证得△ABF≌△EDG(SAS),得出∠AFB=∠DGE=∠HGC,证得H、F、C、G四点共圆,得出∠AHE=∠C=90°,由HD为直角三角形斜边上的中线,即可得出结论.
解答 证明:∵四边形ABCD是正方形,
∴∠DBC=45°,
∵FG∥BD,
∴∠CFG=∠DBC=45°,
∵∠C=90°,
∴△FGC是等腰直角三角形,
∴BF=BC-FC=CD-CG=DG,
在△ABF和△EDG中,$\left\{\begin{array}{l}{AB=AD=DE}\\{∠ABF=∠EDG=90°}\\{BF=DG}\end{array}\right.$,
∴△ABF≌△EDG(SAS),
∴∠AFB=∠DGE=∠HGC,
∴∠HFC+∠HGC=180°,
∴H、F、C、G四点共圆,
∴∠AHE=∠C=90°,
∴△AHE为直角三角形,
∵DE=AD,
∴HD为斜边上的中线,
∴HD=AD.
点评 本题考查了正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、四点共圆、圆内接四边形的性质、直角三角形斜边上的中线性质等知识,本题综合性强,难度较大,通过证明三角形全等和四点共圆才能得出结论.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
20.下列方程中,关于x的一元二次方程是( )
| A. | (x+1)2=2(x+1) | B. | $\frac{1}{x^2}+\frac{1}{x}-2=0$ | C. | ax2+bx+c=0 | D. | x2+2x=x2-1 |
11.关于x的一元二次方程x2-ax=5的一个根是-1,则a的值是(( )
| A. | -1 | B. | 1 | C. | 4 | D. | -4 |

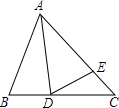 己知:如图,等边△ABC中,D、E分别是BC、AC上的点,且∠ADE=60°
己知:如图,等边△ABC中,D、E分别是BC、AC上的点,且∠ADE=60°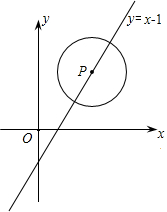 如图,已知⊙P的半径为1,圆心P在直线y=x-1的图象上运动.当⊙P与x轴相切时,则P点的坐标为(2,1)或(0,-1).
如图,已知⊙P的半径为1,圆心P在直线y=x-1的图象上运动.当⊙P与x轴相切时,则P点的坐标为(2,1)或(0,-1).