题目内容
13.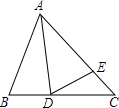 己知:如图,等边△ABC中,D、E分别是BC、AC上的点,且∠ADE=60°
己知:如图,等边△ABC中,D、E分别是BC、AC上的点,且∠ADE=60°(1)求证:△ABD∽△DCE;
(2)若BD=1,EC=3,求△ABC的周长.
分析 (1)由△ABC是等边三角形,得到∠ABD═∠DCE=60°,根据∠ADE=60°,得到∠ADB=∠CED,即可得到结论;
(2)根据相似三角形的性质得到$\frac{AB}{CD}=\frac{BD}{CE}$,设AB=x,则CD=x-4,代入比例式即可求出结论.
解答 (1)证明:∵△ABC是等边三角形,
∴∠ABD═∠DCE=60°,
∵∠ADE=60°,
∴∠ADB=120°-∠CDE,∠CED=120°-∠CDE,
∴∠ADB=∠CED,
∴△ABD∽△DCE;
(2)解:∵△ABD∽△DCE,
∴$\frac{AB}{CD}=\frac{BD}{CE}$,
设AB=x,则CD=x-4,
∴$\frac{x}{x-4}=\frac{4}{3}$,
解得x=16,
∴△ABC的周长=48.
点评 本题考查了相似三角形的判定和性质,三角形的周长的求法,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
 如图所示,ABCD为正方形,延长AD到E,使DE=AD,FG∥BD,EG交AF于H,证明:HD=AD.
如图所示,ABCD为正方形,延长AD到E,使DE=AD,FG∥BD,EG交AF于H,证明:HD=AD.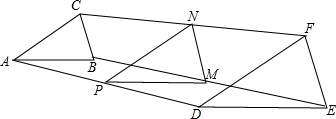
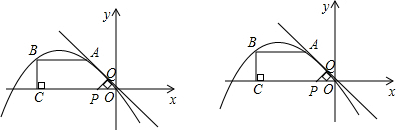
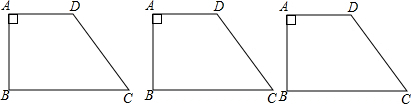
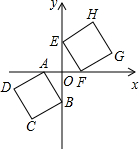 如图,边长均为3的正方ABCD与正方形EFGH在平面直角坐标系中关于原点对称,点A(-1,0).
如图,边长均为3的正方ABCD与正方形EFGH在平面直角坐标系中关于原点对称,点A(-1,0).