Question

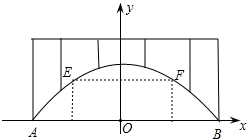廊桥是我国古老的文化遗产，如图，是某座抛物线型的廊桥示意图．已知抛物线的函数表达式为y=-

1

40

x²+10，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E、F处要安装两盏警示灯，求这两盏灯的水平距离EF的长．

Answer 1

考点：二次函数的应用

专题：

分析：已知抛物线上距水面AB高为8米的E、F两点，可知E、F两点纵坐标为8，把y=8代入抛物线解析式，可求E、F两点的横坐标，根据抛物线的对称性求EF长．

解答：解：由于两盏E、F距离水面都是8m，因而两盏景观灯之间的水平距离就
是直线y=8与抛物线两交点的横坐标差的绝对值．
故有-

1

40

x²+10=8，
即x²=80，x₁=4

5

，x₂=-4

5

．
所以两盏警示灯之间的水平距离为：
EF=|x₁-x₂|=|4

5

-（-4

5

）|=8

5

≈18（m）．

点评：本题考查的是二次函数在实际生活中的应用，注意利用函数对称的性质来解决问题．