题目内容
4.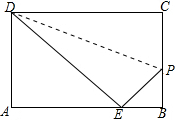 如图,沿PD折叠长方形纸片ABCD的边CD,使点C落在边AB上的点E处,已知AD=8,S△ADE=24,求PB的长.
如图,沿PD折叠长方形纸片ABCD的边CD,使点C落在边AB上的点E处,已知AD=8,S△ADE=24,求PB的长.
分析 首先设PB=xcm,则PE=CP=(8-x)cm.由勾股定理得:PB2+EB2=PB2求出x的值即可得出答案.
解答 解:∵BC=AD=8,S△ADE=24,
∴AE=6,
由勾股定理得:AE2+AD2=DE2
∴DE=CD=AB=10,
∴BE=AB-AE=4
设PB=xcm,则PE=CP=(8-x)cm.
由勾股定理得:PB2+BE2=PE2
∴x2+42=(8-x)2
解得:x=3,
∴PB=3.
点评 此题考查了矩形的性质、折叠的性质以及勾股定理等知识.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
13.两个连续奇数的平方差一定是( )
| A. | 2的倍数,但不一定是4的倍数 | B. | 4的倍数,但不一定是8的倍数 | ||
| C. | 8的倍数,但不一定是16的倍数 | D. | 16的倍数,但不一定是32的倍数 |
 △ABC中,AB=8,AC=3,AC是BC边上的中线,则AD长度的取值范围是2.5cm<AD<5.5cm.
△ABC中,AB=8,AC=3,AC是BC边上的中线,则AD长度的取值范围是2.5cm<AD<5.5cm. 如图,在每个小正方形的边长均为1的方格纸中有线段AB和CD,其中点A、B、C、D均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中有线段AB和CD,其中点A、B、C、D均在小正方形的顶点上.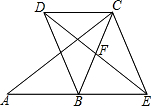 如图,在△ABC中,点F是BC的中点,点E是线段AB的延长线上的动点,连接EF,过点C作AE的平行线,与线段EF的延长线交于点D,连接CE、BD.
如图,在△ABC中,点F是BC的中点,点E是线段AB的延长线上的动点,连接EF,过点C作AE的平行线,与线段EF的延长线交于点D,连接CE、BD. 如图,在宽为40米的一条绿化带上开一条路,数据如图所示,求这条路的宽度.
如图,在宽为40米的一条绿化带上开一条路,数据如图所示,求这条路的宽度.