题目内容
19.若方程组$\left\{\begin{array}{l}{x+2y=m}\\{2x+y=1}\end{array}\right.$的解满足x-y=7,则m的值-6.分析 方程组中第二个方程与已知方程联立求出x与y的值,代入方程组中第一个方程即可求出m的值.
解答 解:根据题意联立得:$\left\{\begin{array}{l}{2x+y=1①}\\{x-y=7②}\end{array}\right.$,
①+②得:3x=8,即x=$\frac{8}{3}$,
把x=$\frac{8}{3}$代入②得:$\frac{8}{3}$-y=7,即y=-$\frac{13}{3}$,
将x=$\frac{8}{3}$,y=-$\frac{13}{3}$代入x+2y=m得:m=$\frac{8}{3}$-$\frac{26}{3}$=-6,
故答案为:-6.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.多边形的边数增加1时、它的内角和与外角和( )
| A. | 都不变 | B. | 内角和增加180°外角和不变 | ||
| C. | 都增加180° | D. | 内角和增加180°外角和减少180° |
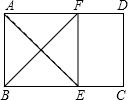 如图,在矩形ABCD中,∠A的平分线交BC于E,∠B的平分线交AD于F,求证:四边形ABEF是正方形.
如图,在矩形ABCD中,∠A的平分线交BC于E,∠B的平分线交AD于F,求证:四边形ABEF是正方形.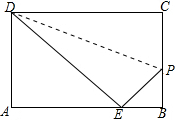 如图,沿PD折叠长方形纸片ABCD的边CD,使点C落在边AB上的点E处,已知AD=8,S△ADE=24,求PB的长.
如图,沿PD折叠长方形纸片ABCD的边CD,使点C落在边AB上的点E处,已知AD=8,S△ADE=24,求PB的长.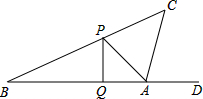 如图:小明同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.
如图:小明同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.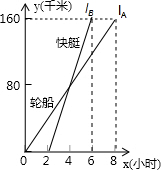 如图,一艘轮船(A)和一艘快艇(B)沿相同路线从甲港出发到乙港,图中lA和lB分别表示A、B行驶过程中路程y(km)与时间x(h)变化之间的函数关系,根据图象解答下列问题:
如图,一艘轮船(A)和一艘快艇(B)沿相同路线从甲港出发到乙港,图中lA和lB分别表示A、B行驶过程中路程y(km)与时间x(h)变化之间的函数关系,根据图象解答下列问题: 如图,已知直线a∥b,c⊥d,∠1=36°,则∠2的度数是126°.
如图,已知直线a∥b,c⊥d,∠1=36°,则∠2的度数是126°.