题目内容
14. △ABC中,AB=8,AC=3,AC是BC边上的中线,则AD长度的取值范围是2.5cm<AD<5.5cm.
△ABC中,AB=8,AC=3,AC是BC边上的中线,则AD长度的取值范围是2.5cm<AD<5.5cm.
分析 延长AD到E,使AD=DE,连接BE,证△ADC≌△EDB,推出EB=AC,根据三角形的三边关系定理求出即可.
解答 解: 延长AD到E,使AD=DE,连接BE,
延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
∵$\left\{\begin{array}{l}{BD=CD}\\{∠ADC=∠BDE}\\{AD=DE}\end{array}\right.$,
∴△ADC≌△EDB(SAS),
∴EB=AC=3,
根据三角形的三边关系定理:8cm-3cm<AE<8cm+3cm,
∴2.5cm<AD<5.5cm,
故答案为:2.5cm<AD<5.5cm.
点评 本题主要考查对全等三角形的性质和判定,三角形的三边关系定理,关键是正确作出辅助线,构造全等三角形,掌握三角形两边之和大于第三边,三角形的两边差小于第三边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.多边形的边数增加1时、它的内角和与外角和( )
| A. | 都不变 | B. | 内角和增加180°外角和不变 | ||
| C. | 都增加180° | D. | 内角和增加180°外角和减少180° |
19.在?ABCD中,下列条件不能判断ABCD是正方形的是( )
| A. | ∠ABC=90°且AB=AD | B. | AB=AC且AC⊥BD | C. | AC⊥BD且AC=BD | D. | AC=BD且AB=BC |
3.下列调查中,适合采用抽样调查的是( )
| A. | 调查一批英雄牌钢笔的使用寿命 | |
| B. | 调查本班同学的身高 | |
| C. | 为保证某种新研发的战斗机成功试飞,对其零部件进行检查 | |
| D. | 对乘坐高铁的乘客进行安检 |
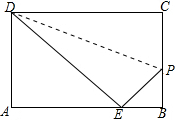 如图,沿PD折叠长方形纸片ABCD的边CD,使点C落在边AB上的点E处,已知AD=8,S△ADE=24,求PB的长.
如图,沿PD折叠长方形纸片ABCD的边CD,使点C落在边AB上的点E处,已知AD=8,S△ADE=24,求PB的长.