题目内容
12.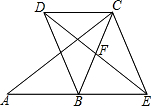 如图,在△ABC中,点F是BC的中点,点E是线段AB的延长线上的动点,连接EF,过点C作AE的平行线,与线段EF的延长线交于点D,连接CE、BD.
如图,在△ABC中,点F是BC的中点,点E是线段AB的延长线上的动点,连接EF,过点C作AE的平行线,与线段EF的延长线交于点D,连接CE、BD.(1)求证:四边形DBEC是平行四边形.
(2)若AB=BC=2,∠ABC=120°,则在点E的运动过程中:
①当BE=1时,四边形DBEC是矩形;
②当BE=2时,四边形DBEC是菱形.
分析 (1)由AAS证明△CDF≌△BEF,得出DF=EF,即可证出四边形DBEC是平行四边形.
(2)①由矩形的性质得出∠AEC=90°,得出∠BCE=30°,由含30°角的直角三角形的性质得出CE=$\frac{1}{2}$BC=1即可;
②由菱形得出BE=CE,证出△BCE是等边三角形,得出BE=BC=2.
解答 (1)证明:∵CD∥AE,
∴∠CDF=∠BEF,
∵点F是BC的中点,
∴CF=BF,
在△CDF和△BEF中,$\left\{\begin{array}{l}{∠CDF=∠BEF}&{\;}\\{∠CFD=∠BFE}&{\;}\\{CF=BF}&{\;}\end{array}\right.$,
∴△CDF≌△BEF(AAS),
∴DF=EF,
∴四边形DBEC是平行四边形.
(2)解:∵AB=BC=2,∠ABC=120°,
∴∠A=∠BCA=30°,
∴∠CBE=30°+30°=60°,
①若四边形DBEC是矩形,
则∠AEC=90°,
∴∠BCE=90°-60°=30°,
∴CE=$\frac{1}{2}$BC=1,
∴当BE=1时,四边形DBEC是矩形;
故答案为:1;
②若四边形DBEC是菱形,则BE=CE,
∵∠CBE=60°,
∴△BCE是等边三角形,
∴BE=BC=2;
∴当BE=2时,四边形DBEC是菱形;
故答案为:2.
点评 本题考查了平行四边形的判定、菱形的判定、矩形的判定、全等三角形的判定与性质;熟练掌握平行四边形的判定,证明三角形全等是解决问题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
3.下列调查中,适合采用抽样调查的是( )
| A. | 调查一批英雄牌钢笔的使用寿命 | |
| B. | 调查本班同学的身高 | |
| C. | 为保证某种新研发的战斗机成功试飞,对其零部件进行检查 | |
| D. | 对乘坐高铁的乘客进行安检 |
20.小明在家中利用物理知识称量某个品牌纯牛奶的净含量,称得六盒纯牛奶的含量分别为:248mL,250mL,249mL,251mL,249mL,253mL,对于这组数据,下列说法正确的是( )
| A. | 平均数为251mL | B. | 中位数为249mL | C. | 众数为250mL | D. | 方差为$\frac{8}{3}$ |
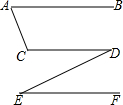 如图所示,∠A+∠C=180°,∠D=∠E,求证:AB∥EF.
如图所示,∠A+∠C=180°,∠D=∠E,求证:AB∥EF.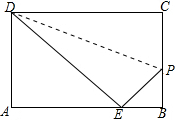 如图,沿PD折叠长方形纸片ABCD的边CD,使点C落在边AB上的点E处,已知AD=8,S△ADE=24,求PB的长.
如图,沿PD折叠长方形纸片ABCD的边CD,使点C落在边AB上的点E处,已知AD=8,S△ADE=24,求PB的长.