题目内容
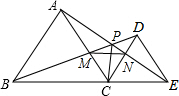 如图,已知点B、C、E在同一条直线上且△ABC与△DEC都是等边三角形,下列结论中,正确的是
如图,已知点B、C、E在同一条直线上且△ABC与△DEC都是等边三角形,下列结论中,正确的是(1)BD=AE;(2)∠BPA=60°;(3)MN∥BE;(4)PN=PA.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)正确;证明△BCD≌△ACE,即可得出BD=AE;
(2)正确;由△BCD≌△ACE,得出∠BDC=∠AEC,由外角关系证出∠APB=60°;
(3)正确;证明△MCD≌△NCE,得出MC=NC,证出△MNC是等边三角形,得出∠NMC=∠ACB,证出MN∥BE;
(4)不正确;由AB∥CD,得出△ABP∽△DNP,
=
,若PA=PN,则AB=DN,显然不成立.
(2)正确;由△BCD≌△ACE,得出∠BDC=∠AEC,由外角关系证出∠APB=60°;
(3)正确;证明△MCD≌△NCE,得出MC=NC,证出△MNC是等边三角形,得出∠NMC=∠ACB,证出MN∥BE;
(4)不正确;由AB∥CD,得出△ABP∽△DNP,
| AB |
| DN |
| PA |
| PN |
解答:解:(1)正确;
∵△ABC和△DEC是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
∴△BCD≌△ACE(SAS),
∴BD=AE,∠BDC=∠AEC;
(2)正确;
∵∠APB=∠PBC+∠AEC,∠DCE=∠PBC+∠BDC=60°,
∴∠APB=60°;
(3)正确;
∵∠ACB=∠DCE=60°,
∴∠MCN=60°,
∴∠MCN=∠DCE=60°,
在△MCD和△NCE中,
∴△MCD≌△NCE(ASA),
∴MC=NC,
∴△MNC是等边三角形,
∴∠NMC=60°,
∴∠NMC=∠ACB,
∴MN∥BE;
(4)不正确;
∵∠ABC=∠DCE,
∴AB∥CD,
∴△ABP∽△DNP,
∴
=
,
若PA=PN,则AB=DN,
显然不成立;∴PN=PA不成立.
故答案是:(1)(2)(3).
∵△ABC和△DEC是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
|
∴△BCD≌△ACE(SAS),
∴BD=AE,∠BDC=∠AEC;
(2)正确;
∵∠APB=∠PBC+∠AEC,∠DCE=∠PBC+∠BDC=60°,
∴∠APB=60°;
(3)正确;
∵∠ACB=∠DCE=60°,
∴∠MCN=60°,
∴∠MCN=∠DCE=60°,
在△MCD和△NCE中,
|
∴△MCD≌△NCE(ASA),
∴MC=NC,
∴△MNC是等边三角形,
∴∠NMC=60°,
∴∠NMC=∠ACB,
∴MN∥BE;
(4)不正确;
∵∠ABC=∠DCE,
∴AB∥CD,
∴△ABP∽△DNP,
∴
| AB |
| DN |
| PA |
| PN |
若PA=PN,则AB=DN,
显然不成立;∴PN=PA不成立.
故答案是:(1)(2)(3).
点评:本题考查了等边三角形的判定与性质以及全等三角形的判定与性质;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
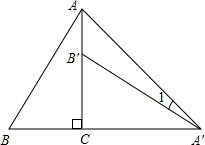 如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C′,连结AA′,若∠1=22°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C′,连结AA′,若∠1=22°,则∠B的度数是( )| A、68° | B、67° |
| C、62° | D、57° |
观察下面由正整数组成的数阵:

照此规律,按从上到下、从左到右的顺序,第50行的第50个数是( )

照此规律,按从上到下、从左到右的顺序,第50行的第50个数是( )
| A、2450 | B、2451 |
| C、2550 | D、2551 |
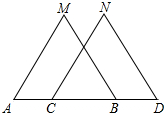 如图,已知A、B、C、D四点在同一直线上,AM=CN,BM=DN,∠M=∠N,
如图,已知A、B、C、D四点在同一直线上,AM=CN,BM=DN,∠M=∠N,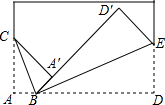 如图,将长方形纸片的一角折叠,使顶点A落在点A′处,折痕CB;再将长方形纸片的另一角折叠,使顶点D落在点D′处,D′在BA′的延长线上,折痕EB.
如图,将长方形纸片的一角折叠,使顶点A落在点A′处,折痕CB;再将长方形纸片的另一角折叠,使顶点D落在点D′处,D′在BA′的延长线上,折痕EB. 已知A(1,4),B(n,-2)是一次函数y=kx+b的图象和反比例函数y=
已知A(1,4),B(n,-2)是一次函数y=kx+b的图象和反比例函数y= 如图,在直角坐标系中,长方形OABC的边OA在y轴的负半轴上,边OC在x轴的正半轴上,点B的坐标为(8,-4),将长方形沿对角线AC翻折,点B落在点D的位置.那么点D的坐标是
如图,在直角坐标系中,长方形OABC的边OA在y轴的负半轴上,边OC在x轴的正半轴上,点B的坐标为(8,-4),将长方形沿对角线AC翻折,点B落在点D的位置.那么点D的坐标是 已知:如图,∠AOB是平角,∠AOD=40°.
已知:如图,∠AOB是平角,∠AOD=40°.