题目内容
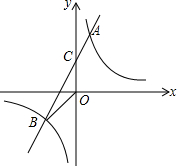 已知A(1,4),B(n,-2)是一次函数y=kx+b的图象和反比例函数y=
已知A(1,4),B(n,-2)是一次函数y=kx+b的图象和反比例函数y=| m |
| x |
(1)求反比例函数和一次函数的关系式;
(2)求△BOC的面积;
(3)直接写出不等式kx+b-
| m |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)由A点在反比例函数y=
上,可求出m,再由A点在函数图象上,由待定系数法求出函数解析式;
(2)由上问求出的函数解析式联立方程求出A,B,C三点的坐标,从而求出△AOC的面积;
(3)由图象观察函数y=
的图象在一次函数y=kx+b图象的上方,对应的x的范围.
| m |
| x |
(2)由上问求出的函数解析式联立方程求出A,B,C三点的坐标,从而求出△AOC的面积;
(3)由图象观察函数y=
| m |
| x |
解答: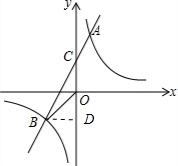 解:(1)∵A(1,4)在反比例函数y=
解:(1)∵A(1,4)在反比例函数y=
的图上,
∴m=4,
又∵B(n,-2)在反比例函数y=
的图象上,
∴n=-2,
又∵B(-2,-2),A(1,4)是一次函数y=kx+b的上的点,联立方程组解得,
k=2,b=2,
∴y=
,y=2x+2;
(2)过点B作BD⊥CD,
∵一次函数y=kx+b的图象和反比例函数y=
的图象的两个交点为A,B,联立方程组解得,
A(1,4),B(-2,-2),C(0,2),
∴BD=2,CO=2,
∴△BOC的面积为:S=
BD•CO=
×2×2=2;
(3)由图象知:当0<x<1和-2<x<0时函数y=
的图象在一次函数y=kx+b图象的上方,
∴不等式kx+b-
<0的解集为:0<x<1或x<-2.
 解:(1)∵A(1,4)在反比例函数y=
解:(1)∵A(1,4)在反比例函数y=| m |
| x |
∴m=4,
又∵B(n,-2)在反比例函数y=
| m |
| x |
∴n=-2,
又∵B(-2,-2),A(1,4)是一次函数y=kx+b的上的点,联立方程组解得,
k=2,b=2,
∴y=
| 4 |
| x |
(2)过点B作BD⊥CD,
∵一次函数y=kx+b的图象和反比例函数y=
| m |
| x |
A(1,4),B(-2,-2),C(0,2),
∴BD=2,CO=2,
∴△BOC的面积为:S=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由图象知:当0<x<1和-2<x<0时函数y=
| m |
| x |
∴不等式kx+b-
| m |
| x |
点评:此题考查一次函数和反比例函数的性质及图象,考查用待定系数法求函数的解析式,还间接考查函数的增减性,从而来解不等式.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
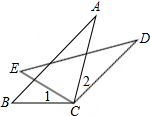 如图,CD=CA,∠1=∠2,EC=BC,与DE相等的线段是哪一条?说明理由.
如图,CD=CA,∠1=∠2,EC=BC,与DE相等的线段是哪一条?说明理由. 如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.过点A作直线AB的垂线交BD的延长线于点E,且AB=
如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.过点A作直线AB的垂线交BD的延长线于点E,且AB=
 已知,如图所示,折叠长方形OABC的一边BC,折痕为CE,使点B落在OA边的点D处,如果AB=8,BC=10.求:
已知,如图所示,折叠长方形OABC的一边BC,折痕为CE,使点B落在OA边的点D处,如果AB=8,BC=10.求: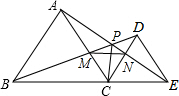 如图,已知点B、C、E在同一条直线上且△ABC与△DEC都是等边三角形,下列结论中,正确的是
如图,已知点B、C、E在同一条直线上且△ABC与△DEC都是等边三角形,下列结论中,正确的是 如图,用一段长为40米的篱笆围成一个一边靠墙的矩形菜园,墙长为22米.
如图,用一段长为40米的篱笆围成一个一边靠墙的矩形菜园,墙长为22米. 如图,直线AB、CD交于点O,∠COE=80°,OA平分∠COE,则∠DOB=
如图,直线AB、CD交于点O,∠COE=80°,OA平分∠COE,则∠DOB=