题目内容
 已知:如图,∠AOB是平角,∠AOD=40°.
已知:如图,∠AOB是平角,∠AOD=40°.(1)求∠BOD的度数;
(2)若OE平分∠BOD,∠BOC是直角,求∠COE的度数.
考点:角平分线的定义
专题:
分析:(1)根据平角的定义可得∠BOD=180°-∠AOD=140°;
(2)由OE平分∠BOD,可得∠BOE=
∠BOD=70°,再根据∠COE=∠BOC-∠BOE即可求解.
(2)由OE平分∠BOD,可得∠BOE=
| 1 |
| 2 |
解答:解:(1)∵∠AOB是平角,∠AOD=40°,
∴∠BOD=180°-∠AOD=140°;
(2)∵OE平分∠BOD,
∴∠BOE=
∠BOD=70°,
∴∠COE=∠BOC-∠BOE=90°-70°=20°.
∴∠BOD=180°-∠AOD=140°;
(2)∵OE平分∠BOD,
∴∠BOE=
| 1 |
| 2 |
∴∠COE=∠BOC-∠BOE=90°-70°=20°.
点评:本题考查了角平分线定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.也考查了平角的定义,熟知各角之间的和差关系是解答此题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
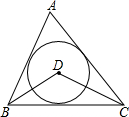 如图,圆O是△ABC的内切圆,∠A=40°,则∠BOC的度数是( )
如图,圆O是△ABC的内切圆,∠A=40°,则∠BOC的度数是( )| A、110° | B、120° |
| C、130° | D、140° |
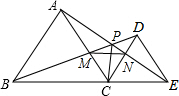 如图,已知点B、C、E在同一条直线上且△ABC与△DEC都是等边三角形,下列结论中,正确的是
如图,已知点B、C、E在同一条直线上且△ABC与△DEC都是等边三角形,下列结论中,正确的是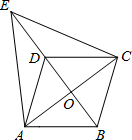 如图,在?ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.
如图,在?ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形. 如图,用一段长为40米的篱笆围成一个一边靠墙的矩形菜园,墙长为22米.
如图,用一段长为40米的篱笆围成一个一边靠墙的矩形菜园,墙长为22米. 如图,有一长方形纸片ABCD,AB=5,AD=13,将此长方形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB,AD(包括端点),设BA′=x,则x的取值范围是
如图,有一长方形纸片ABCD,AB=5,AD=13,将此长方形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB,AD(包括端点),设BA′=x,则x的取值范围是 如图,在△ABC中,AB=AC,若点P为BC延长线上一点,猜一猜:P到两腰的距离之差等于什么?请给出证明.
如图,在△ABC中,AB=AC,若点P为BC延长线上一点,猜一猜:P到两腰的距离之差等于什么?请给出证明.