题目内容
6. 如图,在边长为4cm的正方形ABCD中,一点P由B向C以2cm/s的速度移动,同时又有一点Q由C向D以1cm/s的速度移动,设移动时间为t,当0<t<2时,求△PCQ的面积S(cm2)与时间t(s)之间的函数关系式,并指出是什么函数.
如图,在边长为4cm的正方形ABCD中,一点P由B向C以2cm/s的速度移动,同时又有一点Q由C向D以1cm/s的速度移动,设移动时间为t,当0<t<2时,求△PCQ的面积S(cm2)与时间t(s)之间的函数关系式,并指出是什么函数.
分析 设移动时间为t,则表示出BP=2t,CQ=t,PC=4-2t,然后根据三角形面积公式可得S=-t2+2t(0<t<2),再根据二次函数的定义判断它们的函数关系.
解答 解:设移动时间为t,则BP=2t,CQ=t,PC=4-2t,
所以△PCQ=$\frac{1}{2}$•PC•CQ=$\frac{1}{2}$•(4-2t)•t=-t2+2t,
即△PCQ的面积S(cm2)与时间t(s)之间的函数关系式为S=-t2+2t(0<t<2),S为t的二次函数.
点评 本题考查了动点问题的函数图象:利用速度公式用时间表示相应线段,然后利用面积公式求面积与时间之间函数关系.

练习册系列答案
相关题目
16.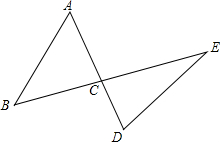 如图,在△ABC中,∠B=45°,∠D=64°,AC=BC,则∠E的度数是( )
如图,在△ABC中,∠B=45°,∠D=64°,AC=BC,则∠E的度数是( )
 如图,在△ABC中,∠B=45°,∠D=64°,AC=BC,则∠E的度数是( )
如图,在△ABC中,∠B=45°,∠D=64°,AC=BC,则∠E的度数是( )| A. | 45° | B. | 26° | C. | 36° | D. | 64° |
11. 如图,已知数轴上的点A、B、O、C、D、E分别表示数-3、-2、0、1、2、3,则表示数-1+$\sqrt{5}$的点P应落在线段( )
如图,已知数轴上的点A、B、O、C、D、E分别表示数-3、-2、0、1、2、3,则表示数-1+$\sqrt{5}$的点P应落在线段( )
 如图,已知数轴上的点A、B、O、C、D、E分别表示数-3、-2、0、1、2、3,则表示数-1+$\sqrt{5}$的点P应落在线段( )
如图,已知数轴上的点A、B、O、C、D、E分别表示数-3、-2、0、1、2、3,则表示数-1+$\sqrt{5}$的点P应落在线段( )| A. | AB上 | B. | OC上 | C. | CD上 | D. | DE上 |
 如图,已知四边形ABCD(网格中每个小正方形的边长均为1).
如图,已知四边形ABCD(网格中每个小正方形的边长均为1).
