题目内容
13.对函数y=$\frac{2}{x}$,下列说法错误的是( )| A. | 它的图象分布在一、三象限 | B. | 当x<0时,y的值对x的增大而减小 | ||
| C. | 它的图象比经过点(-1,-2) | D. | 当x>0时,y的值随x的增大而增大 |
分析 根据反比例函数y=$\frac{2}{x}$的图象上点的坐标特征,以及该函数的图象的性质进行分析、解答.
解答 解:A、因为2>0,所以反比例函数y=$\frac{2}{x}$的图象经过第一、三象限;故本选项正确;
B、当x<0时,反比例函数图象位于第三象限,故在第三象限,y随x的增大而减小;故本选项正确;
C、当x=-1时,y=-2,即点(-1,-2)在反比例函数y=$\frac{2}{x}$的图象上;故本选项正确;
D、因为x>0,所以反比例函数y=$\frac{2}{x}$的图象经过第三象限,且在每一象限内,y随x的增大而减小,本选项错误,
故选D.
点评 本题考查的是反比例函数的性质,即反比例函数y=$\frac{k}{x}$(k≠0)的图象是双曲线,当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.

练习册系列答案
相关题目
1.五一期间,囊阳旅行社组织198人到古隆中和鹿门寺旅游,到古隆中的人数比到鹿门寺的人数2倍少3人,若设到古隆中旅游的人数为x人,到鹿门寺旅游的人数为y人,则可列方程组为( )
| A. | $\left\{\begin{array}{l}{x=2y-3}\\{x+y=198}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2y=x-3}\\{x+y=198}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2(y-3)}\\{x+y=198}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2(y+3)}\\{x+y=198}\end{array}\right.$ |
 如图,等腰Rt△ABC的直角边AB=10cm,点P,Q分别从A,C两点同时出发,均以1cm/s的速度作直线运动.已知点P沿射线AB运动,点Q沿边BC的延长线运动,设点P运动时间为t(s).
如图,等腰Rt△ABC的直角边AB=10cm,点P,Q分别从A,C两点同时出发,均以1cm/s的速度作直线运动.已知点P沿射线AB运动,点Q沿边BC的延长线运动,设点P运动时间为t(s). 如图,点E为DF上一点,点B为AC上一点,且DB∥EC,∠C=∠D,∠A=40°,求∠F的度数.
如图,点E为DF上一点,点B为AC上一点,且DB∥EC,∠C=∠D,∠A=40°,求∠F的度数.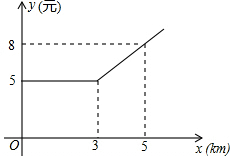 某县出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.
某县出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.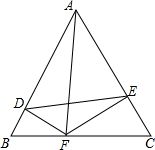 已知△ABC为等边三角形,F为BC上一点,FD⊥AB于D,FE⊥AC于E.求证:$\frac{BF}{CF}=\frac{BD}{CE}$.
已知△ABC为等边三角形,F为BC上一点,FD⊥AB于D,FE⊥AC于E.求证:$\frac{BF}{CF}=\frac{BD}{CE}$.