题目内容
2.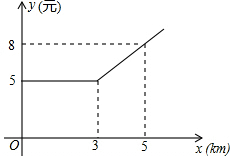 某县出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.
某县出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.(1)出租车的起步价是多少元?
(2)当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
分析 (1)根据函数图象可以得出出租车的起步价是8元;
(2)设当x>3时,y与x的函数关系式为y=kx+b,运用待定系数法就可以求出结论;
(3)将y=32代入(1)的解析式就可以求出x的值.
解答 解:(1)出租车的起步价是5元(3km及以内);
(2)由图象知,y与x的图象为一次函数,并且经过点(3,5),(5,8),
所以如设y与x的关系式为,y=kx+b,
则有:$\left\{\begin{array}{l}{3k+b=5}\\{5k+b=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=\frac{1}{2}}\end{array}\right.$
故y=$\frac{3}{2}$x+$\frac{1}{2}$,
(3)由题意,该乘客乘车里程超过了3km,
$\frac{3}{2}$x+$\frac{1}{2}$=32,
解得:x=21,
所以这位乘客的乘车里程是21km.
点评 本题考查了待定系数法求一次函数的解析式的运用,由函数值求自变量的值的运用,解答时理解函数图象是重点,求出函数的解析式是关键.

练习册系列答案
相关题目
13.对函数y=$\frac{2}{x}$,下列说法错误的是( )
| A. | 它的图象分布在一、三象限 | B. | 当x<0时,y的值对x的增大而减小 | ||
| C. | 它的图象比经过点(-1,-2) | D. | 当x>0时,y的值随x的增大而增大 |
10. 如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )
如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )
 如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )
如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )| A. | x<2 | B. | x>2 | C. | x>1 | D. | x<1 |
7.在△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,则BC边上的高线长是( )
| A. | 3 | B. | 3.6 | C. | 4 | D. | 4.8 |
11.在反比例函数y=$\frac{3}{x}$上的一个点是( )
| A. | (1,2) | B. | (1,3) | C. | (2,6) | D. | (0,0) |
12.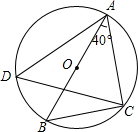 如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
 如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
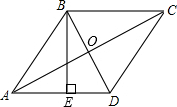 如图,已知菱形对角线BD、AC的长分别为12cm和16cm,求菱形的高BE.
如图,已知菱形对角线BD、AC的长分别为12cm和16cm,求菱形的高BE. A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.