题目内容
3.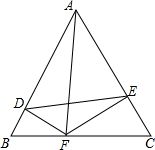 已知△ABC为等边三角形,F为BC上一点,FD⊥AB于D,FE⊥AC于E.求证:$\frac{BF}{CF}=\frac{BD}{CE}$.
已知△ABC为等边三角形,F为BC上一点,FD⊥AB于D,FE⊥AC于E.求证:$\frac{BF}{CF}=\frac{BD}{CE}$.
分析 由等边三角形的性质可得∠B=∠C=60°,由垂直的性质可得∠BDF=∠CEF=90°,进而可证明△FDB∽△FEC,由相似三角形的性质:对应边的比值相等即可证明:$\frac{BF}{CF}=\frac{BD}{CE}$.
解答 证明:∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵FD⊥AB于D,FE⊥AC于E,
∴∠BDF=∠CEF=90°,
∴△FDB∽△FEC,
∴$\frac{BF}{CF}=\frac{BD}{CE}$.
点评 本题考查了相似三角形的判定和性质以及等边三角形的性质,熟记相似三角形的各种判定方法以及其性质是解题关键.

练习册系列答案
相关题目
13.对函数y=$\frac{2}{x}$,下列说法错误的是( )
| A. | 它的图象分布在一、三象限 | B. | 当x<0时,y的值对x的增大而减小 | ||
| C. | 它的图象比经过点(-1,-2) | D. | 当x>0时,y的值随x的增大而增大 |
11.在反比例函数y=$\frac{3}{x}$上的一个点是( )
| A. | (1,2) | B. | (1,3) | C. | (2,6) | D. | (0,0) |
15.点P(-2013,2014)在平面直角坐标系中所在的位置是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.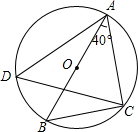 如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
 如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )
如图,AB是圆O的直径,点C、点D在圆O上,连结AC、BC、AD、CD,若∠BAC=40°,则∠ADC的度数等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.