题目内容
5.有A,B两个黑色布袋,A布袋中有两个完全相同的小球,分别标有数字1,2,B布袋中有三个完全相同的小球,分别标有数字1,2,3.小明从A布袋中随机取出一个球记录其标有的数字为x,再从B布袋中随机取出一个球,记录其标有的数字为y,这样就确定点Q的一个坐标为(x,y),点Q落在直线y=-x+3上的概率是$\frac{1}{3}$.分析 根据题意画树状图,然后根据树状图求得所有等可能的结果,即可求得点Q的所有可能坐标.
解答 解:树状图如下:
∴Q点的所有可能是Q(1,1);Q(1,2);Q(1,3);Q(2,1);Q(2,2);Q(2,3),
∵Q(1,2)和(2,1),在直线y=-x+3上,
∴点Q落在直线y=-x+3上的概率为$\frac{1}{3}$.
故答案为:$\frac{1}{3}$
点评 此题考查了列表法或树状图法求概率.注意列表法与树状图法可以不重不漏的表示出所有等可能的结果.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
13.对函数y=$\frac{2}{x}$,下列说法错误的是( )
| A. | 它的图象分布在一、三象限 | B. | 当x<0时,y的值对x的增大而减小 | ||
| C. | 它的图象比经过点(-1,-2) | D. | 当x>0时,y的值随x的增大而增大 |
20.下列调查中,适宜采用抽样调查方式的是( )
| A. | 调查某班学生对“五个重庆”的知晓率 | |
| B. | 调查一架“纤20”隐形战机各零部件的质量 | |
| C. | 调查2016年里约热内卢奥运会100米决赛参赛运动员兴奋剂的使用情况 | |
| D. | 调查涪陵市民对涪陵电视台《晚间播报》栏目的收视率 |
10. 如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )
如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )
 如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )
如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )| A. | x<2 | B. | x>2 | C. | x>1 | D. | x<1 |
15.点P(-2013,2014)在平面直角坐标系中所在的位置是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
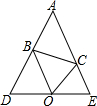 已知:△ABC中,∠ABC与∠ACB外角平分线交于点O,过O作直线交AB,AC延长线于点D,E,且AD=AE.求证:
已知:△ABC中,∠ABC与∠ACB外角平分线交于点O,过O作直线交AB,AC延长线于点D,E,且AD=AE.求证: A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.