题目内容
18.先化简,再求值:$\frac{{m}^{2}-2m+1}{{m}^{2}-1}÷(m-1-\frac{m-1}{m+1})$,其中m是不等式组$\left\{\begin{array}{l}{3m-1≤5}\\{\frac{1-2m}{3}<1}\end{array}\right.$的整数解.分析 先把括号内通分和把除法运算化为乘法运算,再把分子分母因式分解后约分得到原式=$\frac{1}{m}$,接着解不等式求出整数m的值,然后把满足条件的m的值代入计算即可.
解答 解:原式=$\frac{(m-1)^{2}}{(m+1)(m-1)}$÷$\frac{(m-1)(m+1)-(m-1)}{m+1}$
=$\frac{(m-1)^{2}}{(m+1)(m-1)}$•$\frac{m+1}{m(m-1)}$
=$\frac{1}{m}$,
解不等式组$\left\{\begin{array}{l}{3m-1≤5}\\{\frac{1-2m}{3}<1}\end{array}\right.$得-1<m≤2,
所以m为0,1,2,
因为m≠0且m-1≠0,
所以m=2,
当m=2时,原式=$\frac{1}{2}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
13.对函数y=$\frac{2}{x}$,下列说法错误的是( )
| A. | 它的图象分布在一、三象限 | B. | 当x<0时,y的值对x的增大而减小 | ||
| C. | 它的图象比经过点(-1,-2) | D. | 当x>0时,y的值随x的增大而增大 |
10. 如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )
如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )
 如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )
如图,正比例函数y1=$\frac{1}{2}$x与一次函数y2=-2x+5相交于点A(2,1),若y1>y2,那么( )| A. | x<2 | B. | x>2 | C. | x>1 | D. | x<1 |
7.在△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,则BC边上的高线长是( )
| A. | 3 | B. | 3.6 | C. | 4 | D. | 4.8 |
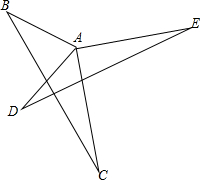 如图,已知AB=AD,AC=AE,∠DAB=90°,∠EAC=90°.说明:
如图,已知AB=AD,AC=AE,∠DAB=90°,∠EAC=90°.说明: 某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取50名女生进行该项目测试,并以测试结果的数据为样本,绘制出如图所示的频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值),已知从左到右各个小长方形的高的比是2:5:8:5:3:2,若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,这次测试的女生中,成绩优秀的共有20人.
某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取50名女生进行该项目测试,并以测试结果的数据为样本,绘制出如图所示的频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值),已知从左到右各个小长方形的高的比是2:5:8:5:3:2,若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,这次测试的女生中,成绩优秀的共有20人.