题目内容
5.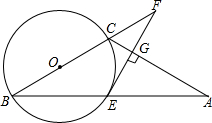 已知,如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
已知,如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.(1)求证:AE=BE;
(2)求证:FE是⊙O的切线;
(3)若FE=4,FC=2,求⊙O的半径及CG的长.
分析 (1)连接CE和OE,因为BC是直径,所以∠BEC=90°,即CE⊥BE;再根据等腰三角形三线合一性质,即可得出结论;
(2)证明OE是△ABC的中位线,得出OE∥AC,再由已知条件得出FE⊥OE,即可得出结论;
(3)由切割线定理求出直径,得出半径的长,由平行线得出三角形相似,得出比例式,即可得出结果.
解答 (1)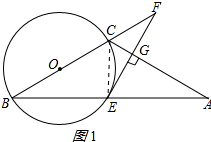 证明:连接CE,如图1所示:
证明:连接CE,如图1所示:
∵BC是直径,
∴∠BEC=90°,
∴CE⊥AB;
又∵AC=BC,
∴AE=BE.
(2)证明:连接OE,如图2所示:
∵BE=AE,OB=OC,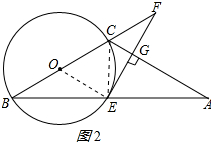
∴OE是△ABC的中位线,
∴OE∥AC,AC=2OE=6.
又∵EG⊥AC,
∴FE⊥OE,
∴FE是⊙O的切线.
(3)解:∵EF是⊙O的切线,∴FE2=FC•FB.
设FC=x,则有2FB=16,
∴FB=8,
∴BC=FB-FC=8-2=6,
∴OB=OC=3,
即⊙O的半径为3;
∴OE=3,
∵OE∥AC,
∴△FCG∽△FOE,
∴$\frac{CG}{OE}=\frac{FC}{FO}$,
即$\frac{CG}{3}=\frac{2}{2+3}$,
解得:CG=$\frac{6}{5}$.
点评 本题考查了切线的判定、等腰三角形的性质、三角形中位线的判定、切割线定理、相似三角形的判定与性质;熟练掌握切线的判定,由三角形中位线定理得出OE∥AC是解决问题的关键.

练习册系列答案
相关题目
13.为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表:
这一天5路公共汽车平均每班的载客量是多少?
请阅读下列探究问题,回答下列问题:
(1)这里的组中值指什么,它是怎样确定的?组中值是上下限之间的中点数值,组中值是指这个小组的两个端点的数的平均数
(2)第二组数据的频数5指什么呢?载客量x落在21≤x<41中的数据个数
(3)如果每组数据在本组中分布较为均匀,则各组数据的平均值和组中值有什么关系.相等.
| 载客量/人 | 组中值 | 频数(班次) |
| 1≤x<21 | 11 | 3 |
| 21≤x<41 | 31 | 5 |
| 41≤x<61 | 51 | 20 |
| 61≤x<81 | 71 | 22 |
| 81≤x<101 | 91 | 18 |
| 101≤x<121 | 111 | 15 |
请阅读下列探究问题,回答下列问题:
(1)这里的组中值指什么,它是怎样确定的?组中值是上下限之间的中点数值,组中值是指这个小组的两个端点的数的平均数
(2)第二组数据的频数5指什么呢?载客量x落在21≤x<41中的数据个数
(3)如果每组数据在本组中分布较为均匀,则各组数据的平均值和组中值有什么关系.相等.
20.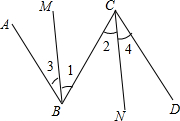 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )| A. | ∠1=∠2 | B. | ∠1=∠3且∠2=∠4 | ||
| C. | BM∥CN | D. | ∠1与∠2互补且不相等 |
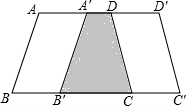 如图,在梯形ABCD中,AD∥BC,AD=4cm,BC=6cm.梯形ABCD的高为5cm、试问将梯形ABCD沿着AD方向平移多少厘米才能使平移后的梯形与原来的梯形ABCD重叠部分的面积为10cm2?
如图,在梯形ABCD中,AD∥BC,AD=4cm,BC=6cm.梯形ABCD的高为5cm、试问将梯形ABCD沿着AD方向平移多少厘米才能使平移后的梯形与原来的梯形ABCD重叠部分的面积为10cm2?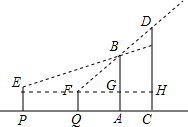 如图,两棵人树AB、CD,它们根部的距离AC=4m.小强沿着正对这两棵树的方向前进,如果小强的眼睛与地面的距离为1.6m,小强在P处时测得B的仰角为20.3°,当小强前进5m达到Q处时,视线恰好经过两棵树的顶部B和D,此时仰角为36.42°.
如图,两棵人树AB、CD,它们根部的距离AC=4m.小强沿着正对这两棵树的方向前进,如果小强的眼睛与地面的距离为1.6m,小强在P处时测得B的仰角为20.3°,当小强前进5m达到Q处时,视线恰好经过两棵树的顶部B和D,此时仰角为36.42°.
 如图,点D在AC的垂直平分线上,AB∥CD,若∠ADC=130°,则∠BAC的度数是25°.
如图,点D在AC的垂直平分线上,AB∥CD,若∠ADC=130°,则∠BAC的度数是25°.