题目内容
12．将抛物线y=x2向上平移4个单位长度，再向右平移1个单位长度后，得到的抛物线的解析式为（ ）| A． | y=（x+1）2+4 | B． | y=（x-1）2+4 | C． | y=（x+4）2-1 | D． | y=（x-4）2 |
分析 抛物线y=x2的顶点坐标为（0，0），向上平移4个单位长度，再向右平移1个单位长度，所得的抛物线的顶点坐标为（1，4），根据顶点式可确定所得抛物线解析式．
解答 解：依题意可知，原抛物线顶点坐标为（0，0），
平移后抛物线顶点坐标为（1，4），
又因为平移不改变二次项系数，
所以所得抛物线解析式为：y=（x-1）2+4．
故选B．
点评 本题考查了二次函数图象与几何变换，属于基础题，解决本题的关键是得到新抛物线的顶点坐标．
练习册系列答案
相关题目
2．木工师傅想利用木条制作一个直角三角形的工具，那么下列各组数据不符合直角三角形的三边长的是（ ）
| A． | 3，4，5 | B． | 6，8，10 | C． | 5，12，13 | D． | 13，16，18 |
3．定义新运算符号“*”的运算过程为a*b=$\frac{1}{2}a-\frac{1}{3}$b，
（1）求2*3的值为0；
（2）若（-3）*x=7，求x的值；
（3）试解方程 2*（2*x）=1*x．
（1）求2*3的值为0；
（2）若（-3）*x=7，求x的值；
（3）试解方程 2*（2*x）=1*x．
20．如果两个三角形相似，其中一个三角形的两个内角分别为82°、53°，那么另一个三角形中最小的内角为 （ ）
| A． | 82° | B． | 53° | C． | 45° | D． | 不能确定 |
17．（-0.5）2013×22014的计算结果正确的是（ ）
| A． | -1 | B． | 1 | C． | -2 | D． | 2 |
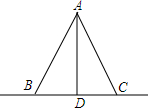如图所示，用两根钢索加固直立的电线杆，若要使钢索AB与AC的长度相等，需添条件BD=CD，理由是线段垂直平分线上的点到线段两端点的距离相等．