题目内容
1.已知一元二次方程x2-3x+m=0.(1)若方程有两个不相等的实数根,求m的取值范围.
(2)若方程有两个相等的实数根,求此时方程的根.
分析 (1)利用方程有两个不相等的实数根,则△>0,建立关于m的不等式,求出m的取值范围;
(2)首先根据方程有两个相等的实数根求出m的值,进而解方程求出方程的根.
解答 解:(1)∵一元二次方程x2-3x+m=0有两个不相等的实数根,
∴△=b2-4ac=9-4m>0,
∴m<$\frac{9}{4}$;
(2)∵一元二次方程x2-3x+m=0有两个相等的实数根,
∴△=b2-4ac=9-4m=0,
∴m=$\frac{9}{4}$;
∴x2-3x+$\frac{9}{4}$=0,
∴x1=x2=$\frac{3}{2}$.
点评 本题主要考查了根的判别式的知识,解答本题要掌握一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
11.下列说法错误的是( )
| A. | 互为相反数的和等于零 | B. | 有理数包括整数和分数 | ||
| C. | 近似数3千和3000的精确度相同 | D. | 近似数0.023精确到千分位 |
12.将抛物线y=x2向上平移4个单位长度,再向右平移1个单位长度后,得到的抛物线的解析式为( )
| A. | y=(x+1)2+4 | B. | y=(x-1)2+4 | C. | y=(x+4)2-1 | D. | y=(x-4)2 |
9.实数-2016的绝对值是( )
| A. | 2016 | B. | -2016 | C. | ±2016 | D. | $\frac{1}{2016}$ |
 如图,抛物线y1=-x2+2向右平移1个单位得到的抛物线y2.回答下列问题:
如图,抛物线y1=-x2+2向右平移1个单位得到的抛物线y2.回答下列问题: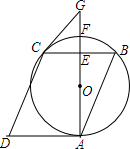 如图,四边形ABCD是平行四边形,点A,B,C在⊙O上,AD与⊙O相切于点A,射线AO交BC于点E,交⊙O于点F,点G在射线AF上,且∠GCB=2∠BAF.
如图,四边形ABCD是平行四边形,点A,B,C在⊙O上,AD与⊙O相切于点A,射线AO交BC于点E,交⊙O于点F,点G在射线AF上,且∠GCB=2∠BAF.