Question

3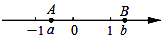．有理数a，b在数轴上对应的位置如图所示，那么代数式$\frac{|a+1|}{a+1}$+$\frac{|b-a|}{a-b}$-$\frac{1-b}{|1-b|}$的值是（　　）

• A． -1
• B． 0
• C． 1
• D． 2

Answer 1

分析 根据图示，可得-1＜a＜0，b＞1，所以a+1＞0，b-a＞0，1-b＜0，据此求出代数式$\frac{|a+1|}{a+1}$+$\frac{|b-a|}{a-b}$-$\frac{1-b}{|1-b|}$的值是多少即可．

解答 解：根据图示，可得-1＜a＜0，b＞1，
∴a+1＞0，b-a＞0，1-b＜0，
∴$\frac{|a+1|}{a+1}$+$\frac{|b-a|}{a-b}$-$\frac{1-b}{|1-b|}$
=$\frac{a+1}{a+1}$+$\frac{b-a}{a-b}$-$\frac{1-b}{b-1}$
=1-1+1
=1
故选：C．

点评 此题主要考查了数轴的特征和应用，以及绝对值的含义和应用，要熟练掌握，解答此题的关键是要明确：①当a是正有理数时，a的绝对值是它本身a；②当a是负有理数时，a的绝对值是它的相反数-a；③当a是零时，a的绝对值是零．