题目内容
8．在直角坐标系中，如果点A沿x轴翻折后能够与点B（-1，4）重合，那么A，B两点之间的距离等于8．分析 首先依据关于x轴对称点的坐标特点可求得点A的坐标，然后依据点A和点B的坐标可求得A、B两点之间的距离．
解答 解：∵点A与点B关于x轴对称，B（-1，4），
∴点A的坐标为（-1，-4）．
∴AB=4-（-4）=4+4=8．
所以A，B两点之间的距离等于8．
故答案为：8．
点评 本题主要考查的是翻折变换、坐标与图形的变化，依据关于x轴对称点的坐标特点求得点A的坐标是解题的关键．
练习册系列答案
相关题目
18．一条直线上有n个点，则以这n个点为端点的射线共有（ ）
| A． | n条 | B． | （n+1）条 | C． | （n+2）条 | D． | 2n条 |
3．
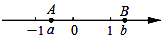有理数a，b在数轴上对应的位置如图所示，那么代数式$\frac{|a+1|}{a+1}$+$\frac{|b-a|}{a-b}$-$\frac{1-b}{|1-b|}$的值是（ ）
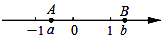有理数a，b在数轴上对应的位置如图所示，那么代数式$\frac{|a+1|}{a+1}$+$\frac{|b-a|}{a-b}$-$\frac{1-b}{|1-b|}$的值是（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
如图，一拱桥呈抛物线状，桥的最大高度是16m，跨度是40m，求在线段AB上离中心M处15m的地方，桥的高度是多少？
如图，点E、F在BC上，∠A=∠D，AB=DC，∠B=∠C．求证：BE=FC．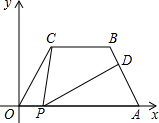
如图所示，在平面直角坐标系中，四边形OABC中BC∥OA，∠COP=∠BAO=60°，OC=AB=4，OA=7，点P为x轴上一个动点，点P不与点O、点A重合．连接CP，过点P作PD交AB于点D．
18．在“石头、剪子、布”的游戏中，当你出“石头”时，对手与你打平的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{4}$ |