题目内容
13.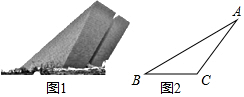 位于合肥滨湖新区的渡江战役纪念馆,实物图如图1所示,示意图如图2所示.某学校数学兴趣小组通过测量得知,纪念馆外轮廓斜坡AB的坡度i=1:$\sqrt{3}$,底基BC=50m,∠ACB=135°,求馆顶A离地面BC的距离.(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
位于合肥滨湖新区的渡江战役纪念馆,实物图如图1所示,示意图如图2所示.某学校数学兴趣小组通过测量得知,纪念馆外轮廓斜坡AB的坡度i=1:$\sqrt{3}$,底基BC=50m,∠ACB=135°,求馆顶A离地面BC的距离.(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 根据题干中给出的角,构造直角三角形.过点A作AD⊥BC交BC的延长线于点D,设AD=x,用x表示出CD、BD,再根据坡度i=1:,列出等量关系式即可得解.
解答  解:如解图,过点A作AD⊥BC交BC的延长线于点D.
解:如解图,过点A作AD⊥BC交BC的延长线于点D.
∵∠ACB=135°,
∴△ADC为等腰直角三角形,
设AD=x,则CD=x,BD=50+x,
∵斜坡AB的坡度i=1:$\sqrt{3}$,
∴x:(50+x)=1:,
整理得($\sqrt{3}$-1)x=50,
解得x=25($\sqrt{3}$+1)≈68.3.
答:馆顶A离地面BC的距离约为68.3 m.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、理解坡度的概念是解题的关键.

练习册系列答案
相关题目
1.-$\frac{1}{4}$的相反数是( )
| A. | 4 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | -4 |
8.已知x2-2x-3=0,则2x2-4x的值为( )
| A. | 6 | B. | -6 | C. | -2或6 | D. | -2或30 |
18.在实数0,(-$\sqrt{3}$)0,(-$\frac{2}{3}$)-2,|-2|中,最大的是( )
| A. | 0 | B. | (-$\sqrt{3}$)0 | C. | (-$\frac{2}{3}$)-2 | D. | |-2| |
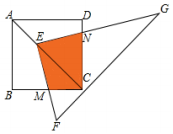 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF,EG分别交BC,DC于点M,N,若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为$\frac{4}{9}$a2.
如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF,EG分别交BC,DC于点M,N,若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为$\frac{4}{9}$a2.