题目内容
13.一元二次方程(1+k)x2-2x+1=0有两个不相等的实数根,则k的取值范围是k<0且k≠-1.分析 根据方程(1+k)x2-2x+1=0有两个不相等的实数根结合根的判别式以及二次项系数非0,即可得出关于k的一元一次不等式组,解不等式组即可得出结论.
解答 解:∵方程(1+k)x2-2x+1=0有两个不相等的实数根,
∴$\left\{\begin{array}{l}{1+k≠0}\\{△=(-2)^{2}-4(1+k)>0}\end{array}\right.$,
解得:k<0且k≠-1.
故答案为:k<0且k≠-1.
点评 本题考查了根的判别式以及解一元一次不等式组,根据方程有两个不相等的实数根结合二次项系数非0得出关于k的一元一次不等式组是解题的关键.

练习册系列答案
相关题目
5.绝对值相等的两个数在数轴上对应的两点距离为6,则这两个数是( )
| A. | 6,-6 | B. | 0,6 | C. | 0,-6 | D. | 3,-3 |
 如图,已知:在△ABC和△DEF中,如果AB=DE,BC=EF,只要找出∠B=∠DEF或AB∥DE,就可证得△ABC≌△DEF.
如图,已知:在△ABC和△DEF中,如果AB=DE,BC=EF,只要找出∠B=∠DEF或AB∥DE,就可证得△ABC≌△DEF. 已知,如图:∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF:
已知,如图:∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF: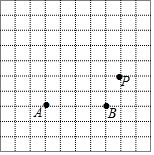 已知A、B两点在小方格的顶点上,位置如图所示.请在小方格的顶点上确定一点C,连结AB、AC、BC,使△ABC为等腰三角形且它的面积为6个平方单位;再用直尺过P作PQ⊥直线AC于点Q.
已知A、B两点在小方格的顶点上,位置如图所示.请在小方格的顶点上确定一点C,连结AB、AC、BC,使△ABC为等腰三角形且它的面积为6个平方单位;再用直尺过P作PQ⊥直线AC于点Q.