题目内容
1．化简：$\frac{3x+2y}{{x}^{2}-{y}^{2}}$-$\frac{2x+y}{{x}^{2}+{y}^{2}}$．分析 原式通分并利用同分母分式的减法法则计算即可得到结果．
解答 解：原式=$\frac{（3x+2y）（{x}^{2}+{y}^{2}）-（2x+y）（{x}^{2}-{y}^{2}）}{（{x}^{2}+{y}^{2}）（{x}^{2}-{y}^{2}）}$．
点评 此题考查了分式的加减法，分式加减法的关键是通分，通分的关键是找最简公分母．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
11．
根据图中数据，计算大长方形的面积，通过不同的计算方法，你发现的结论是（ ）
根据图中数据，计算大长方形的面积，通过不同的计算方法，你发现的结论是（ ）| A． | （a+b）（a+2b）=a2+3ab+2b2 | B． | （3a+b）（a+b）=3a2+4ab+b2 | ||
| C． | （2a+b）（a+b）=2a2+3ab+b2 | D． | （3a+2b）（a+b）=3a2+5ab+2b2 |
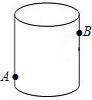如图，圆柱形玻璃容器高20cm，底面圆的周长为48cm，在外侧距下底1cm的点A处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距上口1cm的点B处有一只苍蝇，则蜘蛛捕获苍蝇所走的最短路线长度为30cm．
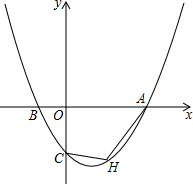如图，已知抛物线y=ax2+bx+c过点A（6，0），B（-2，0），C（0，-3）．