题目内容
9.计算:(1)$\frac{3{a}^{2}bx}{4c{d}^{2}y}•\frac{-10c{y}^{2}}{21a{x}^{3}}$;
(2)(2xy-x2)÷$\frac{x-2y}{xy}$.
(3)6x3y2÷(-$\frac{y}{x}$)•$\frac{x}{{y}^{2}}$÷x2;
(4)(a2-a)÷$\frac{{a}^{2}-2a+1}{a-1}$.
分析 (1)根据分式的乘法,能约分的先约分即可解答本题;
(2)先提公因式,再化简即可解答本题;
(3)把除法转化为乘法再化简即可解答本题;
(4)先提公因式,再把除法转化为乘法,进行计算即可解答本题.
解答 解:(1)$\frac{3{a}^{2}bx}{4c{d}^{2}y}•\frac{-10c{y}^{2}}{21a{x}^{3}}$
=$-\frac{3{a}^{2}bx}{4c{d}^{2}y}•\frac{10c{y}^{2}}{21a{x}^{3}}$
=-$\frac{5aby}{14{d}^{2}{x}^{2}}$;
(2)(2xy-x2)÷$\frac{x-2y}{xy}$
=x(2y-x)×$\frac{xy}{x-2y}$
=-x2y;
(3)6x3y2÷(-$\frac{y}{x}$)•$\frac{x}{{y}^{2}}$÷x2
=-$6{x}^{3}{y}^{2}•\frac{x}{y}•\frac{x}{{y}^{2}}•\frac{1}{{x}^{2}}$
=$-\frac{6{x}^{3}}{y}$;
(4)(a2-a)÷$\frac{{a}^{2}-2a+1}{a-1}$
=a(a-1)×$\frac{a-1}{(a-1)^{2}}$
=a.
点评 本题考查分式的乘除法,解题的关键是明确分式乘除法的计算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{2a}$ | B. | $\sqrt{\frac{b}{3}}$ | C. | $\sqrt{{c}^{3}}$ | D. | $\sqrt{8{d}^{2}}$ |
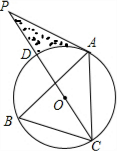 如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.