题目内容
8.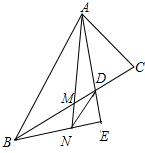 如图,已知△ABC中,M是BC的中点,AD平分∠A,B在AD上的射影为E,EB交AM于N,求证:DN∥AB.
如图,已知△ABC中,M是BC的中点,AD平分∠A,B在AD上的射影为E,EB交AM于N,求证:DN∥AB.
分析 注意到AE既平分∠BAC又垂直BE,延长BE、AC交于点F,根据三线合一可知△ABF是等腰三角形,从而E是BF中点,又由于M是BC中点,连接ME,则ME∥AF,于是$\frac{CM}{MD}=\frac{AE}{DE}$,对于△BDE和截线AMN由梅涅劳斯定理可得$\frac{BM}{MD}•\frac{DA}{AE}•\frac{EN}{NB}=1$,又CM=BM,从而$\frac{CM}{MD}•\frac{DA}{AE}•\frac{EN}{NB}=1$,于是$\frac{AE}{DE}•\frac{DA}{AE}•\frac{EN}{NB}=1$,即$\frac{EN}{NB}=\frac{DE}{DA}$,结论得证.
解答 证明:延长BE、AC交于点F,连接ME,如图: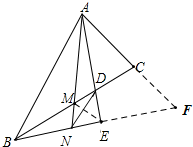
∵AE平分∠BAC,AE⊥BE,
∴BE=EF,
∵BM=CM,
∴EM∥AF,
∴$\frac{CM}{DM}=\frac{AE}{ED}$,
∴$\frac{BM}{DM}=\frac{AE}{ED}$,
对于△BDE和截线AMN,由梅涅劳斯定理可得$\frac{BM}{MD}•\frac{DA}{AE}•\frac{EN}{NB}=1$,
∴$\frac{AE}{DE}•\frac{DA}{AE}•\frac{EN}{NB}=1$,
∴$\frac{DA}{DE}=\frac{NB}{NE}$,
∴DN∥AB.
证毕.
点评 本题主要考查了梅涅劳斯定理的应用、三线合一、中位线、平行线分线段成比例定理及其逆定理等知识点,难度较大,对学生的数学素质要求较高.根据线段AE的“三线合一”特性构造等腰三角形是本题的突破口,后面的工作就是比例推导而已.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.下列说法正确的是( )
| A. | 互为相反数的两数均为一正一负 | B. | 1是最小的正整数 | ||
| C. | 有理数包含正有理数与负有理数 | D. | 一个数的绝对值是正数 |
 在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式.
在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式. 如图,在△ABC中,AB=AC,∠BAC=45°,点D是BC的中点,过点C作CE⊥AB,垂足为点E,交AD于点F.
如图,在△ABC中,AB=AC,∠BAC=45°,点D是BC的中点,过点C作CE⊥AB,垂足为点E,交AD于点F.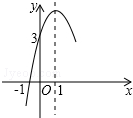 已知抛物线y=ax2+bx+c的部分图象如图所示,则不等式ax2+bx+c>0的解集为-1<x<3.
已知抛物线y=ax2+bx+c的部分图象如图所示,则不等式ax2+bx+c>0的解集为-1<x<3.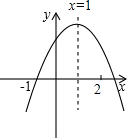 已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c>3b;⑤a+b>m(am+b)(m≠1的实数),其中正确的结论有( )
已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c>3b;⑤a+b>m(am+b)(m≠1的实数),其中正确的结论有( )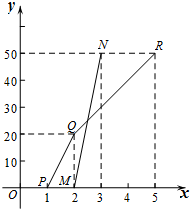 A、B两地相距50km,甲、乙两人在某日同时接到通知,都要从A到B地且行驶路线相同,甲骑自行车从A地出发驶往B地,乙也于同日骑摩托车从A地出发驶往B地,如图折线PQR和线段MN分别表示甲、乙两人所行驶的里程数y(km)与接到通知后的时间t(h)之间的函数关系的图象.
A、B两地相距50km,甲、乙两人在某日同时接到通知,都要从A到B地且行驶路线相同,甲骑自行车从A地出发驶往B地,乙也于同日骑摩托车从A地出发驶往B地,如图折线PQR和线段MN分别表示甲、乙两人所行驶的里程数y(km)与接到通知后的时间t(h)之间的函数关系的图象.