题目内容
1.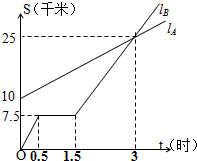 如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.(1)B出发时与A相距10千米.
(2)走了一段路后,自行车发生故障进行修理,所用的时间是1小时.
(3)B出发后3小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)
(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?
分析 (1)根据函数图象可以直接看出B出发时与A相距的路程;
(2)根据函数图象可以得到走了一段路后,自行车发生故障进行修理所用的时间;
(3)根据函数图象可以直接得到B出发后多长时间与A相遇;
(4)根据直线lA经过点(0,10),(3,25)可以求得它的解析式;
(5)根据函数图象可以求得lB的解析式与直线lA联立方程组即可求得相遇的时间.
解答 解:(1)根据函数图象可知,B出发时与A相距10千米,
故答案为:10;
(2)根据函数图象可知,走了一段路后,自行车发生故障进行修理,所用的时间是1.5-0.5=1小时,
故答案为:1;
(3)根据图象可知B出发后3小时时与A相遇;
(4)根据函数图象可知直线lA经过点(0,10),(3,25).
设直线lA的解析式为:S=kt+b,则$\left\{\begin{array}{l}{b=10}\\{3k+b=25}\end{array}\right.$
解得,k=5,b=10
即A行走的路程S与时间t的函数关系式是:S=5t+10;
(5)设直线lB的解析式为:S=kt,
∵点(0.5,7.5)在直线lB上,
∴7.5=k×0.5
得k=15
∴S=15t.
∴$\left\{\begin{array}{l}{S=5t+10}\\{S=15t}\end{array}\right.$
解得S=15,t=1.
故若B的自行车不发生故障,保持出发时的速度前进,1小时时与A相遇.
点评 本题考查一次函数的应用,解体的关键是利用数形结合的思想对图象进行分析,找出所求问题需要的条件.

练习册系列答案
相关题目
13.下列说法正确的是( )
| A. | 互为相反数的两数均为一正一负 | B. | 1是最小的正整数 | ||
| C. | 有理数包含正有理数与负有理数 | D. | 一个数的绝对值是正数 |
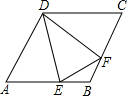 如图,在菱形ABCD中,点E、F分别是AB和BC上的点,且BE=BF,求证:△ADE≌△CDF.
如图,在菱形ABCD中,点E、F分别是AB和BC上的点,且BE=BF,求证:△ADE≌△CDF.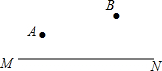 直线MN和同侧两点AB,在MN上找一点P,使得PA+PB最小.(尺规作图)
直线MN和同侧两点AB,在MN上找一点P,使得PA+PB最小.(尺规作图) 如图,在△ABC中,AB=AC,∠BAC=45°,点D是BC的中点,过点C作CE⊥AB,垂足为点E,交AD于点F.
如图,在△ABC中,AB=AC,∠BAC=45°,点D是BC的中点,过点C作CE⊥AB,垂足为点E,交AD于点F.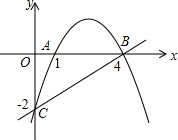 如图,抛物线经过三点A(1,0),B(4,0),C(0,-2).
如图,抛物线经过三点A(1,0),B(4,0),C(0,-2).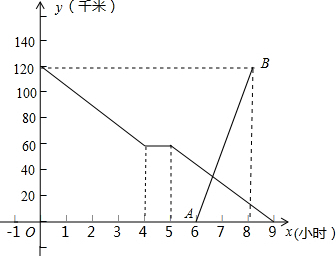 张老师骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶,他距乙地的距离与时间的关系如图中折线所示,李老师骑摩托车沿同一条路匀速从乙地到甲地,比张老师晚出发一段时间,他距乙地的距离与时间的关系如图中线段EF所示.
张老师骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶,他距乙地的距离与时间的关系如图中折线所示,李老师骑摩托车沿同一条路匀速从乙地到甲地,比张老师晚出发一段时间,他距乙地的距离与时间的关系如图中线段EF所示. 如图,E、F为线段AB的三等分点,P为线段AB上一动点(P不与E、F、A、B重合),在点P运动过程中,PE、PF、PA有何数量关系?请写出结论并说明理由.
如图,E、F为线段AB的三等分点,P为线段AB上一动点(P不与E、F、A、B重合),在点P运动过程中,PE、PF、PA有何数量关系?请写出结论并说明理由.