题目内容
11.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.①当点D在AC上时,如图(1),线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;
②将图(1)中的△ADE的位置改变一下,如图(2),使∠BAD=∠CAE,其他条件不变,则线段BD,CE又有怎样的数量关系和位置关系?请说明理由.
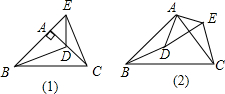
分析 (1)BD=CE,BD⊥CE,延长BD与EC交于点F,可以证明△ACE≌△ADB,可得BD=CE,且∠BFE=90°,即可解答;
(2)BD=CE,BD⊥CE,延长BD交AC于F,交CE于H,可以证明△ACE≌△ADB,可得BD=CE,利用三角形的内角和为180°,即可得到BD⊥CE.
解答 解:(1)BD=CE,BD⊥CE;
如图(1),延长BD与EC交于点F,
在△ACE和△ADB中,
$\left\{\begin{array}{l}{AE=AD}\\{∠EAC=∠DAB}\\{AC=AB}\end{array}\right.$,
∴△ACE≌△ADB(SAS),
∴BD=CE,∠AEC=∠ADB,
∵∠ADB+∠ABD=90°
∴∠ABD+∠AEC=90°
∴∠BFE=90°,
∴BD⊥CE.
(2)结论:BD=CE,BD⊥CE,
理由如下:∵∠BAC=∠DAE=90°
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△ABD与△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$
∴△ABD≌△ACE(SAS)
∴BD=CE,
如图(2),延长BD交AC于F,交CE于H.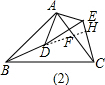
在△ABF与△HCF中,
∵∠ABF=∠HCF,∠AFB=∠HFC
∴∠CHF=∠BAF=90°
∴BD⊥CE.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ACE≌△ADB是解题的关键.

练习册系列答案
相关题目
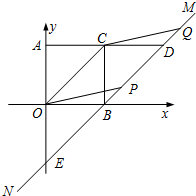 如图,在平面直角坐标系xOy内,?AOBC的顶点A、O、B、C的坐标分别为(0,1)、(0,0)、(1,0)、(1、1),过点B的直线MN与OC平行,AC的延长线交MN于点D,点P是直线MN上的一个动点,CQ∥OP交MN于点Q.
如图,在平面直角坐标系xOy内,?AOBC的顶点A、O、B、C的坐标分别为(0,1)、(0,0)、(1,0)、(1、1),过点B的直线MN与OC平行,AC的延长线交MN于点D,点P是直线MN上的一个动点,CQ∥OP交MN于点Q. 在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式.
在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式. 如图所示.∠AOB=90°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的大小.
如图所示.∠AOB=90°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的大小. 如图,在△ABC中,AB=AC,∠BAC=45°,点D是BC的中点,过点C作CE⊥AB,垂足为点E,交AD于点F.
如图,在△ABC中,AB=AC,∠BAC=45°,点D是BC的中点,过点C作CE⊥AB,垂足为点E,交AD于点F.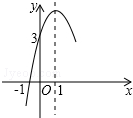 已知抛物线y=ax2+bx+c的部分图象如图所示,则不等式ax2+bx+c>0的解集为-1<x<3.
已知抛物线y=ax2+bx+c的部分图象如图所示,则不等式ax2+bx+c>0的解集为-1<x<3.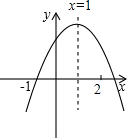 已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c>3b;⑤a+b>m(am+b)(m≠1的实数),其中正确的结论有( )
已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c>3b;⑤a+b>m(am+b)(m≠1的实数),其中正确的结论有( )