题目内容
7. 矩形ABCD的两条对角线相交于点O,∠AOB=60°,AC=4cm,则AB=2cm,矩形ABCD的面积=4$\sqrt{3}$cm2.
矩形ABCD的两条对角线相交于点O,∠AOB=60°,AC=4cm,则AB=2cm,矩形ABCD的面积=4$\sqrt{3}$cm2.
分析 根据矩形性质得出AC=2AO,BD=2BO,AC=BD,推出AO=OB,得出等边三角形AOB,得出AB,由勾股定理求出BC,即可求出矩形ABCD的面积.
解答 解:∵四边形ABCD是矩形,
∴AC=2AO,BD=2BO,AC=BD=4cm,∠ABC=90°,
∴AO=OB=2cm,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=2cm,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$(cm),
∴矩形ABCD的面积=AB•BC=2×2$\sqrt{3}$=4$\sqrt{3}$(cm2);
故答案为:2cm,4$\sqrt{3}$cm2.
点评 本题考查了等边三角形的性质和判定,矩形的性质的应用,勾股定理;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
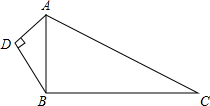 如图,已知AD=6,BD=8,AC=26,BC=24,∠ADB=90°.问△ABC是直角三角形吗?并说明理由.
如图,已知AD=6,BD=8,AC=26,BC=24,∠ADB=90°.问△ABC是直角三角形吗?并说明理由.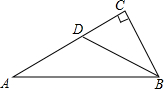 如图所示,在△ABC中,∠C=90°,tanA=$\frac{1}{2}$,D是AC上一点,∠CBD=∠A,sin∠CDB=$\frac{2\sqrt{5}}{5}$.
如图所示,在△ABC中,∠C=90°,tanA=$\frac{1}{2}$,D是AC上一点,∠CBD=∠A,sin∠CDB=$\frac{2\sqrt{5}}{5}$.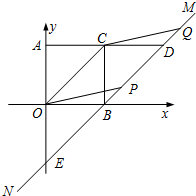 如图,在平面直角坐标系xOy内,?AOBC的顶点A、O、B、C的坐标分别为(0,1)、(0,0)、(1,0)、(1、1),过点B的直线MN与OC平行,AC的延长线交MN于点D,点P是直线MN上的一个动点,CQ∥OP交MN于点Q.
如图,在平面直角坐标系xOy内,?AOBC的顶点A、O、B、C的坐标分别为(0,1)、(0,0)、(1,0)、(1、1),过点B的直线MN与OC平行,AC的延长线交MN于点D,点P是直线MN上的一个动点,CQ∥OP交MN于点Q.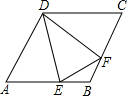 如图,在菱形ABCD中,点E、F分别是AB和BC上的点,且BE=BF,求证:△ADE≌△CDF.
如图,在菱形ABCD中,点E、F分别是AB和BC上的点,且BE=BF,求证:△ADE≌△CDF. 在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式.
在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式. 如图,在△ABC中,AB=AC,∠BAC=45°,点D是BC的中点,过点C作CE⊥AB,垂足为点E,交AD于点F.
如图,在△ABC中,AB=AC,∠BAC=45°,点D是BC的中点,过点C作CE⊥AB,垂足为点E,交AD于点F.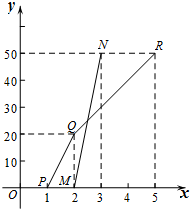 A、B两地相距50km,甲、乙两人在某日同时接到通知,都要从A到B地且行驶路线相同,甲骑自行车从A地出发驶往B地,乙也于同日骑摩托车从A地出发驶往B地,如图折线PQR和线段MN分别表示甲、乙两人所行驶的里程数y(km)与接到通知后的时间t(h)之间的函数关系的图象.
A、B两地相距50km,甲、乙两人在某日同时接到通知,都要从A到B地且行驶路线相同,甲骑自行车从A地出发驶往B地,乙也于同日骑摩托车从A地出发驶往B地,如图折线PQR和线段MN分别表示甲、乙两人所行驶的里程数y(km)与接到通知后的时间t(h)之间的函数关系的图象.