题目内容
13.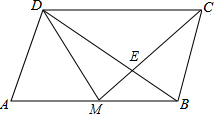 如图,M是?ABCD的边AB的中点,CM与BD相交于点E,求:
如图,M是?ABCD的边AB的中点,CM与BD相交于点E,求:(1)$\frac{{S}_{△CDE}}{{S}_{△BME}}$;
(2)$\frac{{S}_{△BME}}{{S}_{?ABCD}}$.
分析 (1)首先证明△CDE∽△BME,然后根据相似三角形的面积比等于相似比的平方即可求解;
(2)由相似性质得到S△BMC=3S△BME,再由同高图形面积关系得到S?ABCD=4S△BMC=12S△BME,即可求解.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△CDE∽△BME,
∵M是?ABCD的边AB的中点,
∴BM=$\frac{1}{2}$CD,
∴$\frac{CD}{BM}=2$,
∴$\frac{{S}_{△CDE}}{{S}_{△BME}}$=22=4;
(2)∵△CDE∽△BME,
∴$\frac{ME}{EC}=\frac{MB}{CD}=\frac{1}{2}$,
∴S△BMC=3S△BME,
∵M是?ABCD的边AB的中点,
∴S?ABCD=4S△BMC=12S△BME,
∴$\frac{{S}_{△BME}}{{S}_{?ABCD}}$=$\frac{1}{12}$.
点评 本题考查了相似的判定与性质以及等高或等底三角形的面积关系,难度不大;熟练运用三角形相似的性质“相似三角形的面积比等于相似比的平方”是解决问题的关键.

练习册系列答案
相关题目
5.下列运算正确的是( )
| A. | $\frac{{a}^{2}-{b}^{2}}{(a-b)^{2}}=\frac{a+b}{a-b}$ | B. | $\frac{{a}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}}=\frac{a-b}{a+b}$ | ||
| C. | $\frac{x-1}{1-{x}^{2}}=\frac{1}{x+1}$ | D. | $\frac{-x-y}{-x+y}=\frac{x-y}{x+y}$ |
2.将下列多项式因式分解,结果中不含因式x-1的是( )
| A. | x2-1 | B. | x(x-2)+(2-x) | C. | x2-2 | D. | x2-2x+1 |
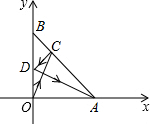 如图,一束光线从点O射出,照在经过A(1,0)、B(0,1)的镜面上的点C,经AB反射后,又照到竖立在y轴位置的镜面上的D点,最后经y轴再反射的光线恰好经过点A,则点C的坐标为($\frac{1}{3}$,$\frac{2}{3}$).
如图,一束光线从点O射出,照在经过A(1,0)、B(0,1)的镜面上的点C,经AB反射后,又照到竖立在y轴位置的镜面上的D点,最后经y轴再反射的光线恰好经过点A,则点C的坐标为($\frac{1}{3}$,$\frac{2}{3}$).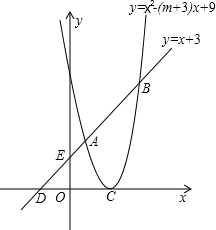 如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴交于D、E两点.
如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴交于D、E两点.