题目内容
4.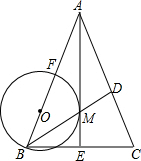 如图,在△ABC中,AB=AC,角平分线AE,BD相交于M,点O在AB边上,以OB为半径的圆恰好经过点M,且与AB相交于另一点F.
如图,在△ABC中,AB=AC,角平分线AE,BD相交于M,点O在AB边上,以OB为半径的圆恰好经过点M,且与AB相交于另一点F.(1)判断AE与⊙O的位置关系,并说明理由.
(2)当BC=4,cosC=$\frac{1}{3}$,求⊙O的半径.
分析 (1)连接OM.利用角平分线的性质和平行线的性质得到AE⊥OM后即可证得AE是⊙O的切线;
(2)通过解直角三角形求得AB=6,设⊙O的半径为R,根据OM∥BE,得到△OMA∽△BEA,利用平行线的性质得到 $\frac{R}{2}$=$\frac{6-R}{6}$,即可解得R=$\frac{3}{2}$,从而求得⊙O的半径为$\frac{3}{2}$.
解答 (1)证明:连接OM.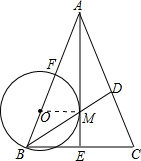
∵AC=AB,AE平分∠BAC,
∴AE⊥BC,CE=BE=$\frac{1}{2}$BC,
∵OB=OM,
∴∠OBM=∠OMB,
∵BM平分∠ABC,
∴∠OBM=∠CBM,
∴∠OMB=∠CBM,
∴OM∥BC,
又∵AE⊥BC,
∴AE⊥OM,
∴AE是⊙O的切线;
(2)∵AB=AC,
∴∠B=∠C,
∵cosC=$\frac{1}{3}$,
∴cosB=$\frac{1}{3}$,
∵CE=BE=$\frac{1}{2}$BC=2,
∴$\frac{BE}{AB}$=$\frac{1}{3}$,
∴AB=6,
设⊙O的半径为R,
∵OM∥BE,
∴△OMA∽△BEA,
∴$\frac{OM}{BE}$=$\frac{AO}{AB}$即 $\frac{R}{2}$=$\frac{6-R}{6}$,
解得R=$\frac{3}{2}$,
∴⊙O的半径为$\frac{3}{2}$.
点评 本题考查了圆的综合知识,题目中还运用到了切线的判定与性质、相似三角形的判定与性质,综合性较强,难度较大.

练习册系列答案
相关题目
14.在函数y=$\sqrt{2-x}$中,自变量x的取值范围是( )
| A. | x≥2 | B. | x≤2 | C. | x>2 | D. | x<2 |
15.不等式x+3>8的解集是( )
| A. | x>5 | B. | x<5 | C. | x=5 | D. | x=-5 |
12.过多边形某个顶点的所有对角线,将这个多边形分成7个三角形,这个多边形是( )
| A. | 八边形 | B. | 九边形 | C. | 十边形 | D. | 十一边形 |
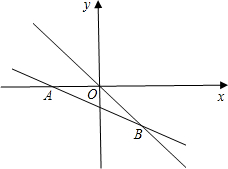 如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{5}$x-$\frac{3\sqrt{3}}{5}$与x轴交于点A,与直线y=-$\frac{\sqrt{3}}{2}$x交于点B.
如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{5}$x-$\frac{3\sqrt{3}}{5}$与x轴交于点A,与直线y=-$\frac{\sqrt{3}}{2}$x交于点B.
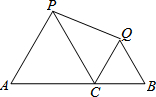 如图,AB=10,C是线段AB上一点,分别以AC、CB为边在AB的同侧作等边△ACP和等边△CBQ,连结PQ,则PQ的最小值是( )
如图,AB=10,C是线段AB上一点,分别以AC、CB为边在AB的同侧作等边△ACP和等边△CBQ,连结PQ,则PQ的最小值是( )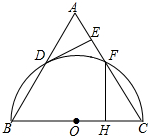 如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.