题目内容
13.已知x1,x2是方程x2-2(k+1)x+4k=0的两根,且-$\frac{3}{2}$<x1<$\frac{1}{2}$.(1)求k的取值范围;
(2)设二次函数y=x2-2(k+1)x+4k的图象与x轴交于A(x1,0),B(x2,0)两点,与y轴交于点M,若OM=OB,求k的值.
分析 (1)先求出方程的两个根,由已知条件即可得出k的取值范围;
(2)分两种情况:①若A(2k,0),B(2,0),由OM=OB得出方程|4k|=2,解方程即可;
②若B(2k,0),A(2,0),得出方程|4k|=|2k|,解方程即可.
解答 解:(1)∵x2-2(k+1)x+4k=0,
∴(x-2)(x-2k)=0,
∴x1=2k,x2=2,
又∵-$\frac{3}{2}$<x1<$\frac{1}{2}$,
∴-$\frac{3}{2}$<2k<$\frac{1}{2}$,即-$\frac{3}{4}$<k<$\frac{1}{4}$;
(2)分两种情况:
①若A(2k,0),B(2,0),
∴OB=2,
又∵M在y轴上,
∴点M的坐标(0,4k),
∴OM=|4k|,
又∵OM=OB,
∴|4k|=2,
解得:k=±$\frac{1}{2}$,
又∵-$\frac{3}{4}$<k<$\frac{1}{4}$,
∴k=-$\frac{1}{2}$;
②若B(2k,0),A(2,0),
则|4k|=|2k|,
解得:k=0;
综上所述:若OM=OB,k的值为-$\frac{1}{2}$或0.
点评 本题考查了一元二次方程的根、抛物线与x轴的交点特征;本题有一定难度,特别是(2)中,需要进行分类讨论,避免漏解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.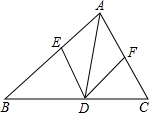 如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )
如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )
 如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )
如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
1.在函数y=$\frac{2}{\sqrt{x}}$中,自变量x的取值范围是( )
| A. | x≥0 | B. | x>0 | C. | x≤0 | D. | x<0 |
5.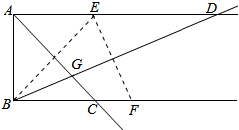 已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )
已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )
 已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )
已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )| A. | ∠AEB+22°=∠DEF | B. | 1+tan∠ADB=$\sqrt{2}$ | C. | 2BC=5CF | D. | 4cos∠AGB=$\sqrt{6}$ |
2.辐射无处不在,我们一年接受的宇宙射线及其它天然辐线照射量约为3100微西弗(1西弗=1000毫西弗,1毫西弗=1000微西弗),用科学记数法可表示为( )
| A. | 3.1×10-6西弗 | B. | 3.1×106西弗 | C. | 3.1×10-3西弗 | D. | 3.1×103西弗 |
3.空气的密度是0.001293g/cm3,这个数用科学记数法可表示为( )
| A. | 1.293×10-3 | B. | -1.293×103 | C. | -12.93×10-2 | D. | 0.1293×10-4 |
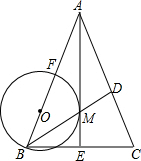 如图,在△ABC中,AB=AC,角平分线AE,BD相交于M,点O在AB边上,以OB为半径的圆恰好经过点M,且与AB相交于另一点F.
如图,在△ABC中,AB=AC,角平分线AE,BD相交于M,点O在AB边上,以OB为半径的圆恰好经过点M,且与AB相交于另一点F. 如图,把一个等边三角形纸片,剪掉一个角后,所得到一个四边形,则图形中∠1+∠2的度数是240°.
如图,把一个等边三角形纸片,剪掉一个角后,所得到一个四边形,则图形中∠1+∠2的度数是240°.