题目内容
15.不等式x+3>8的解集是( )| A. | x>5 | B. | x<5 | C. | x=5 | D. | x=-5 |
分析 根据一元一次不等式解法计算即可.
解答 解:解不等式x+3>8,
可得:x>5,
故选A.
点评 此题考查一元一次不等式解法,关键是根据一元一次不等式解法:移项、合并同类项和系数化为1计算即可.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
5.对于非零的两个实数a、b,规定a⊕b=$\frac{1}{b}$-$\frac{1}{a}$.若1⊕(x+1)=1,则x的值为( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
3.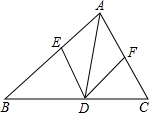 如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )
如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )
 如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )
如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
7.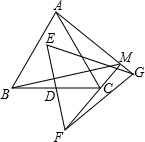 如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( )
如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( )
 如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( )
如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( )| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$+1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$-1 |
5.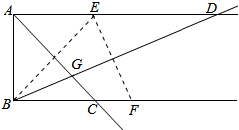 已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )
已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )
 已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )
已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )| A. | ∠AEB+22°=∠DEF | B. | 1+tan∠ADB=$\sqrt{2}$ | C. | 2BC=5CF | D. | 4cos∠AGB=$\sqrt{6}$ |
 如图所示,在直角坐标系中,函数y=$\frac{k}{x}$(x>0,常数k>0)的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C,若点C的坐标为(0,1),则△ABC的面积为1.
如图所示,在直角坐标系中,函数y=$\frac{k}{x}$(x>0,常数k>0)的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C,若点C的坐标为(0,1),则△ABC的面积为1.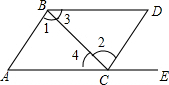 如右图所示,点E在AC的延长线上,如果添一个条件∠3=∠4可以使BD∥AC(只要添一种条件即可)
如右图所示,点E在AC的延长线上,如果添一个条件∠3=∠4可以使BD∥AC(只要添一种条件即可)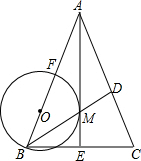 如图,在△ABC中,AB=AC,角平分线AE,BD相交于M,点O在AB边上,以OB为半径的圆恰好经过点M,且与AB相交于另一点F.
如图,在△ABC中,AB=AC,角平分线AE,BD相交于M,点O在AB边上,以OB为半径的圆恰好经过点M,且与AB相交于另一点F.