题目内容
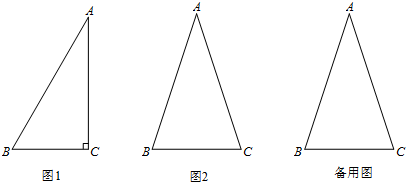
9.我们学习了锐角三角函数的相关知识,知道锐角三角函数定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长的比与角的大小之间可以相互转化.如图1,在Rt△ABC中,∠C=90°.若∠A=30°,则cosA=$\frac{∠A\;的邻边}{斜边}=\frac{AC}{AB}=\frac{{\sqrt{3}}}{2}$.类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对.如图2,在△ABC中,AB=AC,顶角A的正对记作sadA,这时,sadA=$\frac{底边}{腰}=\frac{BC}{AB}$.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述角的正对的定义,解答下列问题:
(1)直接写出sad60°的值为1;
(2)若0°<∠A<180°,则∠A的正对值sad A的取值范围是0<sadA<2;
(3)如图2,已知tanA=$\frac{3}{4}$,其中∠A为锐角,求sadA的值;
(4)直接写出sad36°的值为$\frac{\sqrt{5}-1}{2}$.
分析 (1)根据等腰三角形的性质,求出底角的度数,判断出三角形为等边三角形,再根据正对的定义解答进而得出sad90°的值;
(2)求出0度和180度时等腰三角形底和腰的比即可;
(3)过点B作BD⊥AC于点D,利用勾股定理即可解答;
(4)作出等腰△ABC,构造等腰三角形BCD,根据正对的定义解答.
解答 解:(1)根据正对定义,
当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,
则sad60°=$\frac{1}{1}$=1.
故答案为:1;
(2)当∠A接近0°时,sadA接近0,
当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.
于是sadA的取值范围是0<sadA<2.
故答案为:0<sadA<2.
(3)如图2,过点B作BD⊥AC于点D.
∴∠ADB=∠CDB=90°.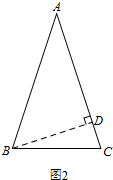
在Rt△ADB中,tanA=$\frac{3}{4}$,
∴设BD=3k,则AD=4k.
∴AB=$\sqrt{B{D^2}+A{D^2}}=5k$.
∵AB=AC,
∴CD=k.
∴在Rt△CDB中,利用勾股定理得,BC=$\sqrt{10}k$.
在等腰△ABC中,sad A=$\frac{BC}{AB}=\frac{{\sqrt{10}k}}{5k}=\frac{{\sqrt{10}}}{5}$.
(4)如图3所示:已知:∠A=36°,AB=AC,BC=BD,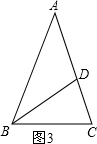
∴∠A=∠CBD=36°,∠ABC=∠C=72°,
∴△BCD∽△ABC,
∴$\frac{BC}{AC}=\frac{CD}{BC}$,
∴$\frac{BC}{BC+CD}=\frac{CD}{BC}$,
解得:BC=$\frac{\sqrt{5}+1}{2}$CD,
∴sad36°=$\frac{CD}{BC}=\frac{\sqrt{5}-1}{2}$.
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了解直角三角形:利用三角函数的定义和相似三角形的判定与性质,根据题意得出BC与CD的关系是解题关键.

 阅读快车系列答案
阅读快车系列答案| A. | (x+1)2 | B. | (x+1)(x-1) | C. | (-x+1)(x-1) | D. | (x-1)(x+2) |
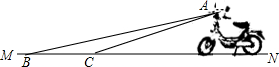 齐河路路通电动车厂新开发的一种电动车如图,它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为8°和10°,大灯A与地面的距离为1m则该车大灯照亮地面的宽度BC是1.4m.(不考虑其它因素)
齐河路路通电动车厂新开发的一种电动车如图,它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为8°和10°,大灯A与地面的距离为1m则该车大灯照亮地面的宽度BC是1.4m.(不考虑其它因素)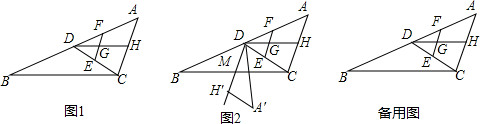 如图1,在△ABC中,CD为AB边上的中线,点E、F分别在线段CD、AD上,且$\frac{DF}{DB}=\frac{DE}{DC}$.点G是EF的中点,射线DG交AC于点H.
如图1,在△ABC中,CD为AB边上的中线,点E、F分别在线段CD、AD上,且$\frac{DF}{DB}=\frac{DE}{DC}$.点G是EF的中点,射线DG交AC于点H.