��Ŀ����
14��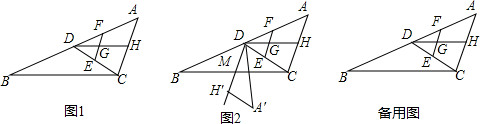 ��ͼ1���ڡ�ABC�У�CDΪAB���ϵ����ߣ���E��F�ֱ����߶�CD��AD�ϣ���$\frac{DF}{DB}=\frac{DE}{DC}$����G��EF���е㣬����DG��AC�ڵ�H��
��ͼ1���ڡ�ABC�У�CDΪAB���ϵ����ߣ���E��F�ֱ����߶�CD��AD�ϣ���$\frac{DF}{DB}=\frac{DE}{DC}$����G��EF���е㣬����DG��AC�ڵ�H����1����֤����DFE�ס�DAC��
��2�������жϵ�H�Ƿ�ΪAC���е㣿��˵�����ɣ�
��3��������ADH�Ƶ�D˳ʱ����ת����A��DH�䣬ʹ����DH��������CB�ཻ�ڵ�M������B��C�غϣ�ͼ2����ת���һ�����Σ�����̽����BMD���BDA��֮���������������ϵ��������֤����
���� ��1�����������ε����ߵĸ�������������ε��ж�����֤�����ɣ�
��2��֤����DGF�ס�DHA����DEG�ס�DCH���������������ε����ʵõ�����ʽ�������߶��е�ĸ���õ�EG=FG�������������ɣ�
��3���ֵ�M���߶�BC�Ϻ͵�M��CB���ӳ���������������������������ε����ʺ���ת�����ʽ�ɣ�
��� ��1��֤������CDΪAB���ϵ����ߣ�
��DB=DA��
��$\frac{DF}{DB}=\frac{DE}{DC}$��
��$\frac{DF}{DA}=\frac{DE}{DC}$���֡�FDE=��ADC��
���DFE�ס�DAC��
��2���⣺��HΪAC���е㣮
�������£��ߡ�DFE�ס�DAC��
���DFE=��DAC��
��EF��AC��
���DGF�ס�DHA����DEG�ס�DCH��
��$\frac{DG}{DH}=\frac{FG}{AH}$��$\frac{DG}{DH}=\frac{EG}{HC}$��
��$\frac{EG}{HC}=\frac{FG}{AH}$��
�ߵ�G��EF���е㣬
��EG=FG��
��HC=AH������HΪAC���е㣻
��3���⣺����ͼ2������M���߶�BC��ʱ������B��C�غϣ���
��BMD+��BDA'=180�㣬
��BD=AD��HC=AH��
��DH��BC��
���BMD=��HDH�䣬
�߽���ADH�Ƶ�D��ת����A'DH'��
���HDH��=��ADA'��
�ߡ�BDA��+��ADA'=180�㣬
���BMD+��BDA��=180�㣻
����ͼ3������M��CB���ӳ�����ʱ����BMD=��BDA'��
��BD=AD��HC=AH��
��DH��BC��
���BMD=��NDH��
�߽���ADH�Ƶ�D��ת����A'DH'��
���HDH��=��ADA'��
�ߡ�BDA��+��ADA'=180�㣬
��NDH+��HDH��=180�㣬
���NDH=��BDA�䣬
���BMD=��BDA�䣮
���� ���⿼��������������ε����ʡ���ת�任�����ʣ��������������ε��ж����������ʶ�����������ת�任�У���ת����ȡ���תǰ���ͼ��ȫ���ǽ���Ĺؼ���

 �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�| A�� | -1 | B�� | -$\sqrt{3}$ | C�� | $\sqrt{3}$ | D�� | 1 |
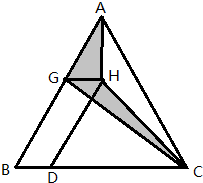 ��ͼ����ABC�����Ϊ16����D��BC����һ�㣬��BD=$\frac{1}{4}$BC����G��AB��һ�㣬��H�ڡ�ABC�ڲ������ı���BDHG��ƽ���ı��Σ���ͼ����Ӱ���ֵ�����ǣ�������
��ͼ����ABC�����Ϊ16����D��BC����һ�㣬��BD=$\frac{1}{4}$BC����G��AB��һ�㣬��H�ڡ�ABC�ڲ������ı���BDHG��ƽ���ı��Σ���ͼ����Ӱ���ֵ�����ǣ�������| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
| A�� | �Ա���� | B�� | �Խ���� | C�� | �Խ������ | D�� | �ڽǺ�Ϊ360�� |
| A�� | 8$\sqrt{a}$ | B�� | $\sqrt{34a}$ | C�� | 8a | D�� | 15$\sqrt{a}$ |
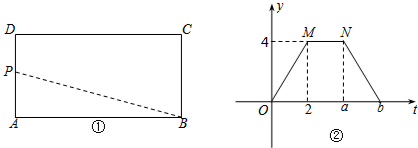
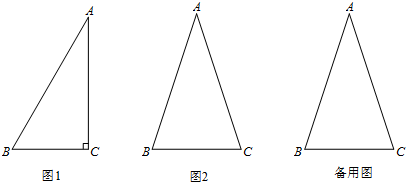
 С��ͬѧ������Ժ�к���һ�����ʿ�����ͻȻ����ǰ�����Ժõ�һ��С���������Ĵ������ˣ���ͼ����С�������С������ʱ��ͻȻ�����ܷ���ѧ������ѧ֪ʶ���С�������������ļнǣ��ܷ����С���������˶��ٶȣ������С����һ�룮
С��ͬѧ������Ժ�к���һ�����ʿ�����ͻȻ����ǰ�����Ժõ�һ��С���������Ĵ������ˣ���ͼ����С�������С������ʱ��ͻȻ�����ܷ���ѧ������ѧ֪ʶ���С�������������ļнǣ��ܷ����С���������˶��ٶȣ������С����һ�룮