题目内容
16.若实数x,y,z满足:|x3+8|+(y-$\sqrt{3}$)2+$\sqrt{z-4}$=0,则yx+z=3.分析 根据非负数的性质列式求出x、y、z的值,然后代入代数式进行计算即可得解.
解答 解:由题意得,x3+8=0,y-$\sqrt{3}$=0,z-4=0,
解得x=-2,y=$\sqrt{3}$,z=4,
所以,yx+z=($\sqrt{3}$)-2+4=3.
故答案为:3.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程2-(x-a)(x-b)=0的两根,且a<b,则a、b、m、n的大小关系是( )
| A. | a<m<n<b | B. | m<a<b<n | C. | a<m<b<n | D. | m<a<n<b |
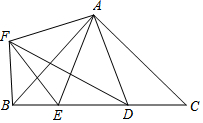 如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,作AF⊥AD,AF=AD,得到△AFB,连接EF.
如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,作AF⊥AD,AF=AD,得到△AFB,连接EF.
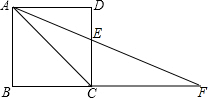 已知,点F在正方形ABCD的边BC的延长线上,且AC=CF,求∠F及∠AEC的度数.
已知,点F在正方形ABCD的边BC的延长线上,且AC=CF,求∠F及∠AEC的度数.