题目内容
3.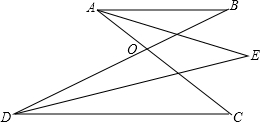 如图,AB∥CD,AC、BD交于点O,∠A、∠D的角平分线交于点E,已知∠E=50°,求∠AOB的度数.
如图,AB∥CD,AC、BD交于点O,∠A、∠D的角平分线交于点E,已知∠E=50°,求∠AOB的度数.
分析 过E点作EF∥AB,根据平行线的性质和角的和差关系得到∠1+∠4=∠E=50°,根据角平分线的定义可得∠BAO+∠CDO=100°,再根据平行线的性质,等量关系和三角形内角和定理即可求解.
解答  解:过E点作EF∥AB,
解:过E点作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠1=∠5,∠4=∠6,
∴∠1+∠4=∠E=50°,
∵∠A、∠D的角平分线交于点E,
∴∠1=∠2,∠3=∠4,
∴∠BAO+∠CDO=100°,
∵AB∥CD,
∴∠B=∠CDO,
∴∠BAO+∠B=100°,
∴∠AOB=180°-100°=80°.
点评 本题考查了平行线的性质,角平分线的定义,三角形内角和定理的知识,难度不大,熟练掌握整体思想是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
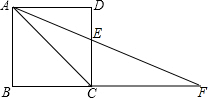 已知,点F在正方形ABCD的边BC的延长线上,且AC=CF,求∠F及∠AEC的度数.
已知,点F在正方形ABCD的边BC的延长线上,且AC=CF,求∠F及∠AEC的度数. 如图,若要得到AD∥EF,需要添加的条件是(只填一个条件)∠2=∠3.
如图,若要得到AD∥EF,需要添加的条件是(只填一个条件)∠2=∠3.