题目内容
16.抛物线y=x2+bx+4的图象向右平移3个单位,再向上平移2个单位所得到的图象解析式为y=x2-2x+c,则bc=12.分析 先用b表示出抛物线y=x2+bx+4的顶点坐标,再求出平移后的抛物线顶点坐标,再用c表示出抛物线y=x2-2x+c的顶点坐标,两顶点坐标相对比求出b、c的值即可.
解答 解:∵抛物线y=x2+bx+4的顶点坐标为(-$\frac{b}{2}$,$\frac{16-{b}^{2}}{4}$),
∴向右平移3个单位,再向上平移2个单位后的坐标为(-$\frac{b}{2}$+3,$\frac{16-{b}^{2}}{4}$+2).
∵平移后图象的解析式为y=x2-2x+c,
∴顶点坐标为(1,c-1),
∴$\left\{\begin{array}{l}{-\frac{b}{2}+3=1}\\{\frac{{16-b}^{2}}{4}+2=c-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=4}\\{c=3}\end{array}\right.$,
∴bc=12.
故答案为:12.
点评 本题考查的是二次函数的图象与几何变换,熟知“上加下减,左加右减”的法则是解答此题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
6.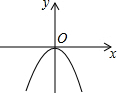 已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
 已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
4.已知G是△ABC的重心,且GP∥BC交AB于点P,BC=3$\sqrt{3}$,则GP的长为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
8.在如图中,表示数轴正确的是( )
| A. |  | B. |  | C. |  | D. |  |
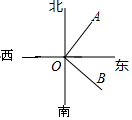 如图,在点O北偏东65°的某处有一点A,在点O南东20°的某处有一点B,则∠AOB的度数是95°.
如图,在点O北偏东65°的某处有一点A,在点O南东20°的某处有一点B,则∠AOB的度数是95°.