题目内容
11.当三角形中一个内角β是另一个内角α的$\frac{1}{2}$时,我们称此三角形为”希望三角形“,其中角α称为”希望角“.如果一个”希望三角形“中有一个内角为54°,那么这个”希望三角形“的”希望角“度数为54°或84°或108°.分析 分54°角是α、β和既不是α也不是β三种情况,根据希望角的定义以及三角形的内角和定理列式计算即可得解.
解答 解:①54°角是α,则希望角度数为54°;
②54°角是β,则$\frac{1}{2}$α=β=54°,
所以,希望角α=108°;
③54°角既不是α也不是β,
则α+β+54°=180°,
所以,α+$\frac{1}{2}$α+54°=180°,
解得α=84°,
综上所述,希望角度数为54°或84°或108°.
故答案为:54°或84°或108°.
点评 本题考查了三角形的内角和定理,读懂题目信息,理解希望角的定义是解题的关键,难点在于分情况讨论.

练习册系列答案
相关题目
6.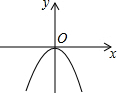 已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
 已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |

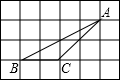 如图,△ABC的顶点都是正方形网格的格点,求∠BAC的三个三角函数值.
如图,△ABC的顶点都是正方形网格的格点,求∠BAC的三个三角函数值. 如图,AE是△BAC的平分线,ED⊥AB于E,EF⊥AC于F,S△ABC=9,DE=2,AB=4,则AC的长为5.
如图,AE是△BAC的平分线,ED⊥AB于E,EF⊥AC于F,S△ABC=9,DE=2,AB=4,则AC的长为5.