题目内容
14.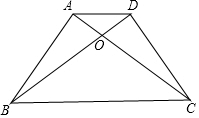 如图所示,AB⊥AC,DC⊥BD,AB=DC,求证:△ABD≌△DCA.
如图所示,AB⊥AC,DC⊥BD,AB=DC,求证:△ABD≌△DCA.
分析 根据全等三角形的判定得出△ABO≌△DCO,根据全等三角形的性质得出∠ABD=∠DCA,AO=DO,BO=CO,求出BD=CA,再根据全等三角形的判定得出即可.
解答 证明:∵AB⊥AC,DC⊥BD,
∴∠BAO=∠CDO=90°,
在△ABO和△DCO中
$\left\{\begin{array}{l}{∠BAO=∠CDO}\\{∠AOB=∠DOC}\\{AB=DC}\end{array}\right.$
∴△ABO≌△DCO(AAS),
∴∠ABD=∠DCA,AO=DO,BO=CO,
∴BD=CA,
在△ABD和△DCA中
$\left\{\begin{array}{l}{AB=DC}\\{∠ABD=∠DCA}\\{DB=AC}\end{array}\right.$
∴△ABD≌△DCA(SAS).
点评 本题考查了全等三角形的判定和性质的应用,能灵活根据定理进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.等式[(-6)-□]÷(-121)=0中,□表示的数是( )
| A. | 6 | B. | -6 | C. | 0 | D. | 115 |
5.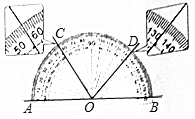 已知直线AB,射线OC,OD都在如图所示的量角器上,点O在直线AB上,则下列判断中不正确的是( )
已知直线AB,射线OC,OD都在如图所示的量角器上,点O在直线AB上,则下列判断中不正确的是( )
 已知直线AB,射线OC,OD都在如图所示的量角器上,点O在直线AB上,则下列判断中不正确的是( )
已知直线AB,射线OC,OD都在如图所示的量角器上,点O在直线AB上,则下列判断中不正确的是( )| A. | ∠AOC=56° | B. | ∠AOD=134° | C. | ∠AOC<∠COD | D. | ∠BOD与∠BOC互补 |
6.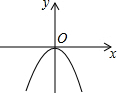 已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
 已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
4.已知G是△ABC的重心,且GP∥BC交AB于点P,BC=3$\sqrt{3}$,则GP的长为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
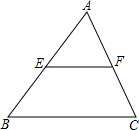 如图,△ABC中,E、F分别是AB、AC的中点,若△AEF的面积为1,则四边形EBCF的面积为3.
如图,△ABC中,E、F分别是AB、AC的中点,若△AEF的面积为1,则四边形EBCF的面积为3.