题目内容
10.解方程(不等式)组:(1)解方程组$\left\{\begin{array}{l}{x-2y=4①}\\{2x+y-3=0②}\end{array}\right.$;
(2)解不等式:$\frac{2x-1}{3}$-$\frac{9x+2}{6}$≤1,并把解集表示在数轴上.
分析 (1)利用代入法即可求解;
(2)去分母、去括号、移项、合并同类项、系数化为1即可求得不等式的解,然后在数轴上表示即可.
解答 解:(1)由①得x=2y+4,
代入②得2(2y+4)+y-3=0,
解得:y=-1,
把y=-1代入x=2y+4得x=2.
则方程组的解集是:$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
(2)去分母,得2(2x-1)-(9x+2)≤1,
去括号,得4x-2-9x-2≤1,
移项,得4x-9x≤2+2+1,
合并同类项,得-5x≤5
系数化成1得x≥-1. .
.
点评 本题考查了方程组的解法和不等式的解法,解方程组的基本思想是消元,方法有代入消元法和加减消元法两种.

练习册系列答案
相关题目
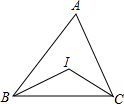 如图,△ABC中,∠A=45°,I是内心,则∠BIC=115°.
如图,△ABC中,∠A=45°,I是内心,则∠BIC=115°. 如图是一台水泵的叶轮平面示意图,它绕着圆心O旋转最小度数为45°后可以与自身重合.
如图是一台水泵的叶轮平面示意图,它绕着圆心O旋转最小度数为45°后可以与自身重合.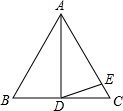 如图,AD是等边三角形ABC的中线,AE=AD,则∠EDC=15°.
如图,AD是等边三角形ABC的中线,AE=AD,则∠EDC=15°.