题目内容
12.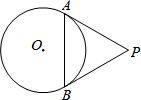 如图,PA、PB分别与相切⊙O于点A、B,连接AB.∠APB=60°,AB=5,则⊙O的半径长为2$\sqrt{3}$.
如图,PA、PB分别与相切⊙O于点A、B,连接AB.∠APB=60°,AB=5,则⊙O的半径长为2$\sqrt{3}$.
分析 首先连接OP,OA,由PA、PB分别与相切⊙O于点A、B,∠APB=60°,易得△ABP是等边三角形,则可求得AP的长,继而求得答案.
解答 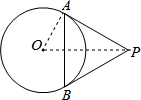 解:连接OA,OP,
解:连接OA,OP,
∵PA、PB分别与相切⊙O于点A、B,
∴PA=PB,OA⊥AB,
∵∠APB=60°,
∴△ABP是等边三角形,
∴PA=AB=6,
∴∠APO=$\frac{1}{2}$∠APB=$\frac{1}{2}$×60°=30°,
∴OA=AP•tan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 此题考查了切线的性质以及等边三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
1. 如图,在?ABCD中,若∠A+∠C=130°,则∠D的大小为( )
如图,在?ABCD中,若∠A+∠C=130°,则∠D的大小为( )
 如图,在?ABCD中,若∠A+∠C=130°,则∠D的大小为( )
如图,在?ABCD中,若∠A+∠C=130°,则∠D的大小为( )| A. | 100° | B. | 105° | C. | 110° | D. | 115° |
17.下列结论错误的是( )
| A. | 等边三角形都相似 | B. | 正方形都相似 | ||
| C. | 所有长方形都相似 | D. | 等腰直角三角形都相似 |
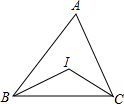 如图,△ABC中,∠A=45°,I是内心,则∠BIC=115°.
如图,△ABC中,∠A=45°,I是内心,则∠BIC=115°. 如图是一台水泵的叶轮平面示意图,它绕着圆心O旋转最小度数为45°后可以与自身重合.
如图是一台水泵的叶轮平面示意图,它绕着圆心O旋转最小度数为45°后可以与自身重合.