题目内容
11.已知二次函数y=kx2-(2k-1)x+k-2的图象与x轴交于两个不同的点,则k的取值范围为k>-$\frac{1}{4}$.分析 因为抛物线与x轴有两个不同的点,所以△>0,列出不等式,解不等式即可解决问题.
解答 解:∵抛物线y=kx2-(2k-1)x+k-2的图象与x轴交于两个不同的点,
∴△>0,
∴(2k-1)2-4k(k-2)>0,
∴k>-$\frac{1}{4}$.
故答案为k>-$\frac{1}{4}$.
点评 本题考查二次函数与x轴的交点问题,记住抛物线与x轴没有交点△<0,抛物线与x轴有两个交点△>0,抛物线与x轴只有一个交点△=0,属于中考常考题型.

练习册系列答案
相关题目
1.下列四张扑克牌中,属于中心对称的图形是( )


| A. | 红桃7 | B. | 方块4 | C. | 梅花6 | D. | 黑桃5 |
6.对于同一平面内的三条直线a,b,c,给出下列5个论断:
①a∥b;②b∥c;③a∥c;④a⊥b;⑤a⊥c.
以其中两个论断作为题设,一个论断作为结论,组成一个你认为不正确的命题是( )
①a∥b;②b∥c;③a∥c;④a⊥b;⑤a⊥c.
以其中两个论断作为题设,一个论断作为结论,组成一个你认为不正确的命题是( )
| A. | 已知①②则③ | B. | 已知②⑤则④ | C. | 已知②④则③ | D. | 已知④⑤则② |
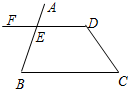 如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.
如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.