题目内容
11.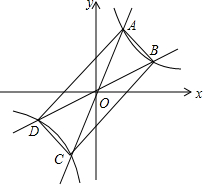 如图,过原点的直线y=k1x和y=k2x与反比例函数y=$\frac{1}{x}$的图象分别交于两点A,C和B,D,连接AB,BC,CD,DA.
如图,过原点的直线y=k1x和y=k2x与反比例函数y=$\frac{1}{x}$的图象分别交于两点A,C和B,D,连接AB,BC,CD,DA.(1)四边形ABCD一定是平行四边形(直接填写结果).
(2)四边形ABCD可能是矩形吗?若可能,试求此时k1和k2之间的关系式;若不可能,说明理由.
分析 (1)由直线y=k1x和y=k2x与反比例函数y=$\frac{1}{x}$的图象关于原点对称,即可得到结论.
(2)联立方程求得A、B点的坐标,然后根据OA=OB,依据勾股定理得出 $\sqrt{\frac{1}{{k}_{1}}+{k}_{1}}$=$\sqrt{\frac{1}{{k}_{2}}+{k}_{2}}$,两边平方得$\frac{1}{{k}_{1}}$+k1=$\frac{1}{{k}_{2}}$+k2,整理后得(k1-k2)(k1k2-1)=0,根据k1≠k2,则k1k2-1=0,即可求得.
解答 解:(1)∵直线y=k1x和y=k2x与反比例函数y=$\frac{1}{x}$的图象关于原点对称,
∴OA=OC,OB=OD,
∴四边形ABCD 是平行四边形;
故答案为:平行;
(2)解:∵正比例函数y=k1x(k1>0)与反比例函数y=$\frac{1}{x}$的图象在第一象限相交于A,
∴k1x=$\frac{1}{x}$,解得x=$\sqrt{\frac{1}{{k}_{1}}}$(因为交于第一象限,所以负根舍去,只保留正根)
将x=$\sqrt{\frac{1}{{k}_{1}}}$带入y=k1x得y=$\sqrt{{k}_{1}}$,
故A点的坐标为($\sqrt{\frac{1}{{k}_{1}}}$,$\sqrt{{k}_{1}}$)同理则B点坐标为($\sqrt{\frac{1}{{k}_{2}}}$,$\sqrt{{k}_{2}}$),
又∵OA=OB,
∴出 $\sqrt{\frac{1}{{k}_{1}}+{k}_{1}}$=$\sqrt{\frac{1}{{k}_{2}}+{k}_{2}}$,两边平方得$\frac{1}{{k}_{1}}$+k1=$\frac{1}{{k}_{2}}$+k2,
整理后得(k1-k2)(k1k2-1)=0,
∵k1≠k2,
所以k1k2-1=0,即k1k2=1.
点评 本题考查了反比例函数的性质,平行四边形的判定,矩形的判定和性质,比较代数式的大小,掌握反比例函数图形上点的坐标的特征是解题的关键.

| A. | 1:2:3:4 | B. | 2:3:2:3 | C. | 2:2:1:1 | D. | 2:3:3:2 |
 如图,在直角坐标系中,∠AOx=60°,∠BOx=135°,OA=2,OB=$\sqrt{2}$,一次函数的图象经过A,B两点,求这个一次函数的表达式.
如图,在直角坐标系中,∠AOx=60°,∠BOx=135°,OA=2,OB=$\sqrt{2}$,一次函数的图象经过A,B两点,求这个一次函数的表达式.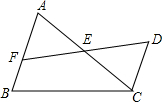 如图,AB∥CD,EF=ED,AB=5,CD=3,则BF=2.
如图,AB∥CD,EF=ED,AB=5,CD=3,则BF=2.